Factoring Trinomials by Grouping `1`

Learning Objective

• Factor polynomials of the form `x^2 + bx + c` by grouping.

A polynomialA monomial or sum of monomials, like `4x^2 + 3x - 10`. with three terms is called a trinomialA three-term polynomial.. Trinomials often (but not always!) have the form `x^2 + bx + c`. At first glance, it may seem difficult to factor trinomials and polynomials with even more terms, but a technique called grouping has the answer. Grouping is a divide-and-conquer strategy—it lets us factor big polynomials a pair of terms at a time instead of all at once.

Let’s start by considering how to use the grouping techniqueA factoring technique involving finding common factors among groups of terms rather than among all of the terms. with four-term polynomials. Then we will apply this method to the special cases of trinomials in the form `x^2 + bx + c`.

When we factor the two-term polynomial `12r^2 - 8r` as `4r(3r - 2)`, we are using the distributive propertyStates that the product of a number and a sum equals the sum of the individual products of the number and the addends: for all real numbers `a`, `b`, and `c`, `a(b + c) = ab + ac`. , which states that `a(b + c) = ab+ac`. We pull out the greatest common factor of two monomialsA number, a variable, or a product of a number and one or more variables with whole number exponents, such as `-5`, `x`, and `8xy^3`. (the `a`), add the factors left behind (the `b + c`), and rewrite the expression as the product of the two. That gives us `a(b + c)`. 

We can apply this same technique to factoring polynomials of three or more terms: wherever we find common factors among monomials, we pull them out and rewrite the expression.

This process is easier when we use the grouping technique. Here's how we do it:

• Group the terms of the polynomial into pairs
• Factor each pair of terms (find their greatest common factor and then use the distributive property to pull out the GCF)
• Look for common factors between the factored forms of the paired terms
• Factor the common polynomial out of the groups

Let's see how that looks in action, when we use the grouping technique to factor a four-term polynomial.

Let’s stop here to take a look at how the original polynomial has changed. The distributive property has been applied twice, creating two terms that are each a product of a monomial and a binomial: `4a(b + 3)` and `3(b + 3)`. Great! But now what?

Notice that the new terms have a common factor: `(b + 3)`. Surely we can make use of that.

Think about how we'd factor `4ax + 3x`. What factors do `4ax` and `3x` share? The greatest common factor is `x`, so we'd pull that factor out and rewrite the polynomial as `x(4a + 3)`. Make sense? Well our polynomial, `4a(b + 3) + 3(b+3)`, is just like that except with `(b + 3)` instead of `x`. So we can factor it the same way, pulling out `(b + 3)` just like we pulled out `x`:

Notice that when we factor `2` terms, the result is a monomial times a polynomial. But the factored form of a `4`-term polynomial is the product of `2` polynomials.

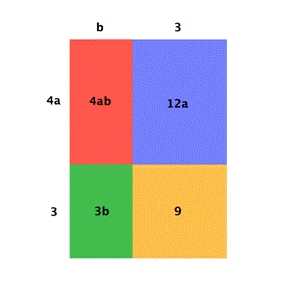
Below is a visual representation of what we just did. Notice how the individual terms in the factors multiply to create the `4` terms of the original polynomial. The entire rectangle has dimensions of `(b + 3)` and `(4a + 3)`. The four smaller rectangles that make up its area are each a different term in the original polynomial. The factored form and the original form of the polynomial are equivalent.

Let’s try factoring one more four-term polynomial. Notice that in the example below, the first term is `x^2`, and `x` is the only variable present—the other examples you have looked at so far have included two variables, but no squared terms.

Notice that both factors here, `(x + 2)` and `(x + 5)`, contain the term `x`. This is often how squared terms are factored, and it leads us nicely into the next topic: factoring trinomials.

Polynomials with three terms are called trinomials. Some trinomials are in the form `x^2 + bx + c`. Trinomials can be factored just like other polynomials, and once again, the key is to use the idea of grouping that we just explored.

Let’s start with the trinomial `x^2 + 7x + 10`. At first glance, it looks like this trinomial cannot be factored, because the individual terms `x^2`, `7x`, and `10` share no common factors. We could pull `x` out of the first two terms, but that would leave us with `x(x + 7) + 10`, which hardly seems helpful.

But let’s look closer… `x^2 + 7x + 10` looks an awful lot like the polynomial `x^2 + 2x + 5x + 10` that we just solved. In fact, if you add `2x` and `5x`, you get `7x`, so the two polynomials are equivalent! And if we factored `x^2 + 2x + 5x + 10` successfully (remember, we arrived at `(x + 2)(x + 5)`) then we should be able to factor `x^2 + 7x + 10` as well. So how do we do it?

Thinking about `x^2 + 7x + 10` as `x^2 + 2x + 5x + 10` actually helps us factor the trinomial, because now we can use groups and the distributive property to pull out common factors. This is one strategy for factoring trinomials in the form `x^2 + bx + c`: expanding the term `bx` into the sum of two quantities.

Great! But wait. How do we know what numbers to break `bx` into? Lucky for us, there's a rule for that:

One way to understand why this method works is to see what happens when the expression `(x + r)(x + s)` is evaluated: it becomes `x^2 + rx + sx + rs`, as shown in the diagram below. The blue square is `x^2`, which is present in both forms of the polynomial. The red rectangle represents `rs` in the expanded, four-term version of the polynomial and `c` in the original trinomial. The two green rectangles stand for `rx + sx` in the expanded form and `bx` in the original expression.

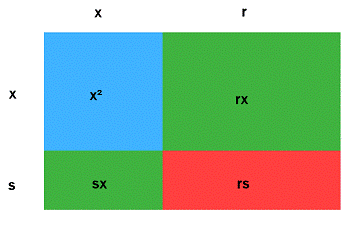
In other words, we've taken the three parts of the trinomial (represented by the three colors of the diagram), and split one of them in two (as shown by the four boxes). The size of the pieces has changed, but the total value is the same.

When we are using this method of factoring trinomials, we are looking for the way to turn three terms into four terms.

Let’s put this method to use and factor the trinomial `a^2 + a - 12`. In this trinomial, the `bx` term is `a` or `1a` and the `c` term is `-12`. (It is important to note that this term is `-12`, not `+12`. This will matter when we find multiplicative pairs!) We want to find two integers, `r` and `s`, whose sum is `1` and whose product is `-12`.

A chart will help us organize possibilities. On the left we'll list all possible factors of `-12`; on the right we'll add the `r` and `s` terms together. Which values for `r` and `s` meet our criteria?

There is only one combination where `r * s = -12` and `r + s = 1`: when `r = 4`, and `s = -3`. Let’s use these to factor our original trinomial.

Factoring trinomials is a matter of practice and patience. Sometimes the appropriate number combinations will just pop out and seem so obvious! Other times, despite trying many possibilities, the correct combinations are hard to find.

While there is no foolproof way to find the right combination on the first guess, there are some tips that can ease the way. Think about why each of these tips is true:

When factoring a four-term polynomial using grouping, find the common factor of pairs of terms rather than the whole polynomial. Use the distributive property to rewrite the grouped terms as the common factor times a binomial. Finally, pull any common binomials out of the factored groups. The fully factored polynomial will be the product of two binomials.

To factor trinomials in the form `x^2 + bx + c`, find two integers, `r` and `s`, whose sum is `b` and whose product is `c`. Rewrite the trinomial as `x^2 + rx + sx + c` and then use grouping and the distributive property to factor the polynomial.