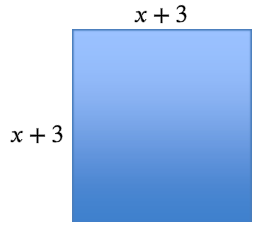
Special Products of Polynomials
Certain types of binomialA sum of two monomials, such as `3x^2 + 7`. multiplication sometimes produce results that are called special productsA product resulting from binomial multiplication that has certain characteristics. For example `x^2 - 25` is called a special product because both its terms are perfect squares and it can be factored into `(x + 5)(x - 5)`. . Special products have predictable terms. Although the distributive property can always be used to multiply any binomials, recognition of those that produce special products provides a problem-solving shortcut.
We call multiplying a number by itself “squaring” because we can represent this multiplication as a square. The number being squared is the length of the side of the square and the product is represented by the area of that square. Consider a square whose side length is described by the binomial `x + 3`:
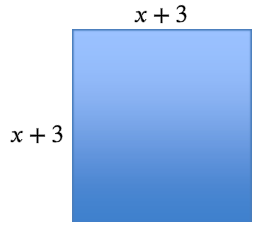
We can zoom into this square and show a little more detail by creating an image that shows the variable and constant terms as follows:

From this area modelA graphic representation of a multiplication problem, in which the length and width of a rectangle are the factors and the area is the product., we can see that the area could be described by the sum of the red, green and yellow pieces. That is, the area is `x^2 + 6x + 9`. So `(x + 3)^2 = x^2 + 6x + 9`.
We can also use what we know about multiplying binomials to find the square of a sum of two terms by using the distributive property. An example is shown below.
|
Example |
|||
|
Problem |
Find `(x + 5)^2`. |
|
|
|
|
`(x + 5)(x + 5)` |
|
Multiply the binomial by itself (square it). |
|
|
`x(x + 5) + 5(x+5)` |
|
Use the distributive property to multiply each term of the first binomial by the second binomial. |
|
|
`x^2 + 5x + 5x + 25` |
|
Group like terms together. |
|
|
`x^2 + 10x + 25` |
|
Combine like terms. |
|
Answer |
`x^2 + 10x + 25` |
|
|
So far, we have two examples of squaring a sum of two terms, one from constructing an area model and one from algebraic calculations:
`(x + 3)^2 = x^2 + 6x + 9`
`(x + 5)^2 = x^2 + 10x + 25`
Notice a pattern? In both cases, the first term in the binomial is squared to get the first term in the product `(x^2 = x^2)`. The last term in the binomial is also squared to get the last term in the product: `3^2 = 9` and `5^2=25`.
Now what about that middle term? Is there a pattern there, too? It isn't as obvious, but there is one. The middle term of the product is twice the product of the terms of the binomial: `2 * 3x = 6x` and `2 * 5x = 10x`.
Let’s look at another example to see if these patterns hold true.
|
Example |
|||
|
Problem |
`(2x+6)^2` |
|
|
|
|
`(2x + 6)(2x + 6)` |
|
Multiply the binomial by itself. |
|
|
`2x(2x + 6) + 6(2x+6)` |
|
Use the distributive property to multiply each term of the first binomial by the second binomial. |
|
|
`4x^2 + 12x + 12x + 36` |
|
Notice there are two `12x` terms. One comes from `2x(x + 6)` and the other comes from `6(2x + 6)`. |
|
|
`4x^2 + 24x+36` |
|
Combine like terms. |
|
Answer |
`4x^2 + 24x+36` |
|
|
The same pattern showed up in this product. The term `2x` is squared to get `4x^2`, and `6` is squared to get `36`. `2x` is multiplied by `6` in two instances, resulting in a term `24x`.
This pattern will hold true for the square of the sum of any two terms and can be generalized as follows:
`(a + b)^2 = a^2 + 2ab + b^2`
Is there also a pattern when you square the difference between two terms? Yes! Since subtraction can be expressed as adding the opposite, a similar pattern does occur.
Consider the square of the binomial `(x - 7)`:
|
Example |
|||
|
Problem |
`(x - 7)^2` |
|
|
|
|
`(x - 7)(x - 7)` |
|
Rewrite as multiplication. |
|
|
`[x + (-7)][x + (-7)]` |
|
Rewrite subtraction of `7` as adding `(-7)`. |
|
|
`x[x + (-7)]+(-7)[x + (-7)]` |
|
Multiply each term in one binomial by the other binomial. |
|
|
`x^2 + (-7)x + (-7)x + 49` |
|
Distribute. |
|
|
`x^2 + (-14)x + 49` |
|
Combine like terms. |
|
Answer |
`x^2 - 14x + 49` |
|
|
If we compare the answer to the original problem, we can see the pattern: the first term, `x`, is squared to get `x^2`. The middle term in the answer is twice the product of `(-7)` and `x`, or `(-14x)`. The last term in the answer is `49`, which is the second term of the binomial, `(-7)`, squared. So, the square of a difference can be generalized as follows:
`(a - b)^2 = a^2 - 2ab + b^2`
Let’s look at an example in which the coefficient is not `1`. Consider the example of squaring the binomial `(4s - 3)`:
|
Example |
|||
|
Problem |
`(4s - 3)^2` |
|
|
|
|
`(4s - 3)(4s - 3)` |
|
Rewrite as multiplication. |
|
|
`16s^2 - 12s - 12s + 9` |
|
Multiply each term in one binomial by the other binomial. |
|
|
`16s^2 - 24s + 9` |
|
Combine like terms. |
|
Answer |
`16s^2 - 24s + 9` |
|
|
Notice that when a variable term has a coefficient, it is included in the multiplication. In the example above, the first term in the answer is the entire first term of the binomial squared `(4s * 4s = 16s^2)`. The second term of the answer is twice the product of both terms of the binomial `2(4s * 3)`. Finally, the last term of the answer is the last term of the binomial squared `(3 * 3 = 9)`.
Sound familiar? It's still the same generalized formula as squaring a difference:
`(a - b)^2 = a^2 - 2ab + b^2`
Just remember that if the first term has a coefficient, it must be included in the multiplication.
|
Find the product: `(2a - 9)^2`
A) `4a^2 - 81`
B) `4a - 18`
C) `4a^2 - 36a + 81`
D) `4a^2 + 18a - 18`
|
There is a third “special” product to consider among binomials. This one arises from multiplication of the sum of two terms by the difference of the same two terms. In this case, there is also a pattern that describes the product. Here is an example:
|
Example |
|||
|
Problem |
`(x + 8)(x - 8)` |
|
|
|
|
`x(x - 8) + 8(x-8)` |
|
Multiply each term in the first binomial by the second binomial. |
|
|
`x^2 - 8x + 8x - 64` |
|
Distribute. |
|
|
`x^2 - 64` |
|
Add like terms. |
|
Answer |
`x^2 - 64` |
|
|
Notice that the answer to this binomial product is a binomial itself—the difference of two perfect squares. There is no middle term in this case. Why does this happen? Because one is a sum and the other is a difference, but otherwise they use the same numbers, the middle terms are opposites (one positive and one negative). They add to zero. The product of a sum and a difference can be generalized as follows:
`(a + b)(a - b) = a^2 - b^2`
|
Special Binomial Products
Product of a Sum: `(a + b)^2 = a^2 + 2ab + b^2`
Product of a Difference: `(a - b)^2 = a^2 - 2ab + b^2`
Product of a Sum and a Difference: `(a + b)(a - b) = a^2 - b^2`
|
Let’s examine the characteristics of polynomials that result from the “special” products we have been discussing. Could we look at a polynomial and tell whether it is the square of a sum or the square of a difference—either `(a + b)^2` or `(a - b)^2` —or the product of a sum and a difference, `(a + b)(a - b)`?
One characteristic of special products is that the first and last terms of these polynomials are always perfect squares (`a^2` and `b^2`). If the first and last terms of a polynomial are perfect squares, the polynomial could be the result of a special product. (To determine if the terms are perfect squares, the polynomial needs to be written with the variable terms in order of decreasing exponents. For example, as `x^2 + 2x + 1`, not `2x + x^2 + 1`.)
If the first and last terms are NOT perfect squares, then the polynomial is not the result of a special product and we can stop looking at other features of the polynomial.
If the first and last terms are perfect squares, we need to look further at other features of the polynomial. We need to see if there is a middle term.
No middle term: If there is no middle term and the binomial is a difference, then the binomial must be the product of a sum and a difference of two terms. Be careful, though, because the binomial MUST be a difference.
|
Example |
|||||||
|
Problem |
Is `16y^2 - t^2` a square of a binomial or a product of a sum and a difference? |
|
|||||
|
|
`16y^2 = (4y)(4y)` `t^2 = t * t`
|
|
Are the first and last terms perfect squares? Yes -- proceed. |
||||
|
|
`16y^2 - t^2` |
|
Is there a middle term in the polynomial? No. This means it could be the product of a sum and a difference.
|
||||
|
|
`16y^2 - t^2`
|
|
Is the binomial a difference? In other words, are the two terms combined by subtraction? Yes. This means the binomial is the product of a sum and a difference of two terms. |
||||
|
Answer |
Yes, `16y^2 - t^2` is the product of a sum and a difference `(4y + t)(4y - t)`. |
|
|
||||
Middle term is present: If there is a middle term in the polynomial, we first check to see if the last term is added or subtracted. If the last term is subtracted, then the polynomial is not the result of a special product and we do not need to examine the polynomial further.
If the last term is added, the polynomial may be a special product and we have to go yet another step further.
Next, we check to see if the middle term is double the product of the square root of the first and the last terms. If the first term is `a^2` and the last term is `b^2`, is the middle term `2ab`? If it is, then the polynomial is either the square of a sum or the square of a difference.
That's quite a list of requirements! Let's try an example and see how it works:
|
Example |
||||||
|
Problem |
Is `4x^2 + 20xy + 25y^2` the square of binomials or the product of a sum and a difference? |
|
||||
|
|
`4x^2 = (2x)(2x)` `25y^2 = (5y)(5y)`
|
|
Are the first and last terms perfect squares? Yes -- proceed. |
|||
|
|
`4x^2 + 20xy + 25y^2`
|
|
Is there a middle term in the polynomial? Yes, `20xy`.
|
|||
|
|
`4x^2 + 20xy + 25y^2`
|
|
Is the last term added in the polynomial? Yes.
|
|||
|
|
`sqrt(4x^2)=2x` `sqrt(25y^2)=5y` `2(2x*5y)=20xy`
|
|
Is the middle term equal to double the product of the square roots of the first and last terms? Yes. `2*sqrt(4x^2)*sqrt(25y^2)=20xy`. This means the polynomial is either the square of a sum or the square of a difference. |
|||
|
Answer |
`4x^2 + 20xy + 25y^2` is the square of a binomial `(2x + 5y)`. |
|||||
|
Which polynomials shown below are special products?
`100x^2 - 25`
`x^2y^2 + 4x + 16`
`y^2 - 18y + 81`
A) All three are special products.
B) Only `100x^2 - 25` and `y^2 - 18y + 81` are special products.
C) Only `100x^2 - 25` and `x^2y^2 + 4x + 16` are special products.
D) None of the polynomials shown is a special product.
|
Some products of multiplying binomials follow a predictable pattern that makes it easy to simplify them. These are known as special products. There are three special products of binomials that each follow a specific formula:
Special Binomial Products
Product of a Sum: `(a + b)^2 = a^2 + 2ab + b^2`
Product of a Difference: `(a - b)^2 = a^2 - 2ab + b^2`
Product of a Sum and a Difference: `(a + b)(a - b) = a^2 - b^2`
Polynomials can be identified as special products by examining the characteristics of their terms.