Resolviendo Sistemas de Ecuaciones Lineales por Sustitución
Objetivos de Aprendizaje
· Definir el método de sustitución.
· Usar el método de sustitución para resolver sistemas de ecuaciones.
Rápido — tienes 5 monedas de un cuarto de dólar, 3 de 5 centavos y una de 10 centavos en tu bolsillo. ¿Cuánto dinero tienes?
Este problema es muy simple, pero pudiste haber usado un poco de álgebra avanzada para resolverlo. ¿Pasaste por el proceso de sumar 25 cinco veces para obtener el valor de los cuartos? ¿O pensaste "Sé que 4 cuartos son $1.00, entonces 5 cuartos deben ser $1.25?
Sustituir un valor conocido por otro valor equivalente es un ejemplo de razonamiento algebraico. Podemos aplicar este método — informalmente llamado método de sustitución — para resolver sistemas de ecuaciones.
Sumar todo tu cambio es simple, Pero problemas complejos se pueden hacer fáciles usando el método de sustitución — sólo busca las cantidades que son iguales y luego usa esas equivalencias para acelerar la solución del problema. Guárdate esos $1.50 en el bolsillo y vamos a trabajar.
Usar la sustitución para resolver problemas te es natural. Fíjate en el siguiente problema:
Sean tiene 5 años más que cuatro veces la edad de su hija. Su hija tiene 7. ¿Cuántos años tiene Sean?
Probablemente puedes resolver este problema mentalmente. La hija de Sean tiene 7 años, y "cuatro veces la edad de su hija" es 28, y otros 5 años es 33. Sean tiene 33 años.
Si resolviste el problema de esa forma, usaste una sustitución simple — sustituiste el valor de "7" por "la edad de su hija." Te dijeron en la segunda parte del problema que "su hija tiene 7." Entonces sustituyendo el valor de "7" por "la edad de su hija" en la primera parte del problema estuvo bien, porque sabías que estas dos cantidades eran iguales.
Intentemos la situación en otro problema más abstracto.
| Ejemplo | |||||||
| Problema | Encontrar el valor de los símbolos, Ψ, y Φ en el sistema siguiente. | ||||||
|
| Ω | = | 3 | ||||
|
| Ω | + | Ψ | + | Ψ | = | 27 |
|
|
| Φ | + | Ω | = | Ψ | |
Este problema se ve distinto al de la edad, pero lo podemos resolver de manera similar. Vemos en la primera ecuación que Ω = 3. Como Ω equivale a 3, podemos sustituir 3 cada vez que vemos Ω en las otras ecuaciones, así:
| Ejemplo | |||||||
| Problema | Encontrar el valor de los símbolos, Ψ, y Φ en el sistema siguiente. | ||||||
|
| Ω | = | 3 | ||||
|
| 3 | + | Ψ | + | Ψ | = | 27 |
|
|
| Φ | + | 3 | = | Ψ | |
Ahora, la segunda ecuación es fácil de resolver: Si 3 + Ψ + Ψ = 27, entonces 2Ψ = 24, y Ψ = 12. Ahora podemos sustituir este valor por Ψ en la última ecuación para encontrar Φ:
| Ejemplo | |||||||
| Problema | Encontrar el valor de los símbolos, Ψ, y Φ en el sistema siguiente. | ||||||
|
| Ω | = | 3 | ||||
|
| 3 | + | Ψ | + | Ψ | = | 27 |
|
|
| Φ | + | 3 | = | 12 | |
| Solución |
|
|
| Φ | = | 9 | |
Si Φ + 3 = 12, entonces Φ = 9. ¡Y ya está! Hemos encontrado los valores de los tres símbolos usando sólo el método de sustitución.
La equivalencia es la idea central en los problemas de sustitución. Si podemos encontrar relaciones equivalentes dentro del sistema, podemos usar esas relaciones para resolver el sistema.
Identificando Equivalencias
En los problemas anteriores, una relación obvia de equivalencia fue presentada para los escenarios: nos dijeron desde el principio que la edad de la hija era de 7 y que el valor de Ω era de 3. No nos fue difícil usar esas relaciones de equivalencia como puntos de partida para resolver los sistemas. Pero ¿qué hacemos en los casos donde las relaciones de equivalencia no son tan obvias? Por ejemplo:
Para vender más producto, una granja local vende bolsas de manzanas de dos tamaños: mediana y grande. Una bolsa mediana contiene 4 manzanas Macintosh y 1 manzana Granny Smith y cuesta $2.80. Una bolsa grande contiene 8 manzanas Macintosh y 4 manzanas Granny Smith y cuesta $7.20. ¿Cuánto cuesta cada uno de los tipos de manzana?
Empecemos por crear un sistema de ecuaciones que represente las dos relaciones en este problema, el costo de cada tipo de manzana en cada bolsa. Usaremos "m" para representar el costo de las manzanas Macintosh, y "g" será el costo de las manzanas Granny Smith. Hagamos una tabla para ver qué es lo que conocemos del sistema y qué es lo que no conocemos:
|
| Costo de las manzanas Macintosh | + | Costo de las manzanas Granny Smith | = | Costo total por bolsa |
| Mediana | 4m | + | g | = | 2.80 |
| Grande | 8m | + | 4g | = | 7.20 |
Si vemos estas ecuaciones, no hay una equivalencia obvia — ambas ecuaciones tienen dos variables. Pero espera — ¿notas que el coeficiente de g es 1 en la primera ecuación? Podemos usar lo que sabemos sobre ecuaciones algebraicas para reescribir la ecuación en términos de g:
| 4m | + | g | = | 2.80 |
|
|
|
|
| g | = | 2.80 | - | 4m |
Ahora tenemos un valor equivalente para g, uno que podemos sustituir por g en la segunda ecuación. Una vez hecho esto, podemos resolver m en la segunda ecuación.
| 8m | + | 4g | = | 7.20 |
| 8m | + | 4(2.80 – 4m) | = | 7.20 |
| 8m | + | 11.20 – 16m | = | 7.20 |
| 8m |
| -16m | = | 7.20 − 11.20 |
|
|
| -8m | = | -4.00 |
|
|
| m | = | 0.50 |
Muy bien, hemos encontrado que m = 0.5, y ahora podemos regresar y sustituir eso en la primera ecuación para calcular el valor de g.
| 4m | + | g | = | 2.80 |
| 4(0.5) | + | g | = | 2.80 |
| 2 | + | g | = | 2.80 |
|
|
| g | = | 2.80 − 2 |
|
|
| g | = | .80 |
Y ahí lo tenemos — el costo de una manzana Macintoch es de 50¢, y el costo de una manzana Granny Smith es de 80¢.
Nota que en la solución anterior hemos resuelto la primera ecuación para la variable g y usado esa equivalencia para "descifrar" el resto del sistema. No hay nada mágico en la razón por la que resolvimos g. Pudimos haber usado cualquiera de las variables en el problema y habríamos llegado al mismo resultado. Otro camino que pudimos haber tomado es el de reescribir la primera ecuación en términos de 4m, y luego sustituir la relación equivalente (4m = 2.80 − g) in la segunda ecuación así:
| 8m | + | 4g | = | 7.20 |
| (2 • 4m) | + | 4g | = | 7.20 |
| (2 • [2.80 − g]) | + | 4g | = | 7.20 |
Resolver g en esta ecuación nos dará el mismo resultado que en el método previo de solución.
Resuelve x y y en el sistema.
2y = x + 9
2y − 11 = 2x
A) x = -3.5, y = 2
B) x = -2, y = 3.5
C) x = -5, y = 2
D) x = 0, y = 4.5
Analizando los Resultados
Hay algunos casos donde el método de sustitución obtiene resultados que, aparentemente, no tienen sentido. Analicemos algunos de estos casos y veamos qué pasa.
Resolver x y y.
y = 5x + 4
10x − 2y = 4
Como la primera ecuación es y = 5x + 4, podemos sustituir 5x + 4 por y en la segunda ecuación.
| 10x | − | 2y | = | 4 |
| 10x | − | 2(5x + 4) | = | 4 |
| 10x | − | 10x + 8 | = | 4 |
| 10x | − | 10x | = | 4 − 8 |
|
|
| 0 | = | -4 |
Esto no tiene sentido. ¿Cómo puede ser 0 = -4? La gráfica del sistema muestra una pista de lo que está pasando:

La razón por la que obtuvimos una respuesta sin sentido es que las rectas son paralelas. Si las rectas nunca se intersectan, no existirá un punto que sea la solución para ambas ecuaciones. El sistema no tiene soluciones.
Ahora veamos este problema, el cual también tiene una solución interesante.
Resolver x y y.
y = -0.5x
9y = -4.5x
Sustituyendo -0.5x por y en la segunda ecuación, encontramos lo siguiente:
| 9y | = | -4.5x |
| 9(-0.5x) | = | -4.5x |
| -4.5x | = | -4.5x |
Esta vez obtenemos una declaración válida: -4.5x = -4.5x. Pero ¿qué significa este tipo de respuesta? Una vez más, la gráfica nos puede ayudar a entender este problema:
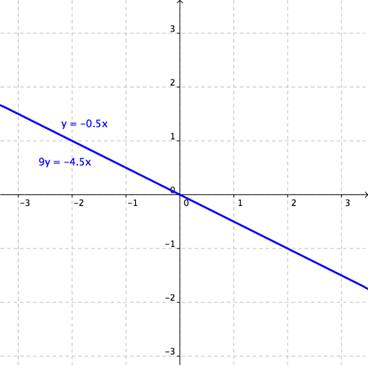
El sistema consiste en dos ecuaciones para la misma recta. Cada punto sobre la línea será una solución del sistema, y es por eso que el método de sustitución nos dio una declaración válida. En este caso, decimos que hay un número infinito de soluciones.
Aubrey está usando el método de sustitución para resolver el siguiente sistema de ecuaciones:
y − x = 21
2y = 2x + 16
Aubrey encuentra la siguiente declaración 8 = 21 y piensa que esto significa que las rectas son paralelas y que el sistema no tiene solución.
Quiere comprobar su respuesta. ¿Cuál de las siguientes acciones le ayudarían mejor para averiguar si las rectas de la ecuación son realmente paralelas?
A) Comprobar si las pendientes de ambas rectas son iguales.
B) Comprobar si alguna de las rectas pasa por el origen.
C) Comprobar si las rectas tienen la misma intersección en y.
D) Comprobar si ambas rectas pasan por el punto (8, 21).
Sumario
El método de sustitución es una manera de resolver sistemas de ecuaciones. Para usar el método de sustitución, primero identificamos relaciones equivalentes dentro del sistema y luego sustituimos esos valores en cada ecuación. La solución de un sistema resuelto por el método de sustitución puede ser de tres tipos: un sólo valor para cada variable en el sistema (indicando una solución), una declaración inválida (indicando 0 soluciones), o una declaración válida (indicando soluciones infinitas).
