Solving Systems of Linear Equations by Substitution

Learning Objectives

• Define the substitution method.
• Use substitution to solve systems of equations.

Quick—you have `5` quarters, `3` nickels, and a dime in your pocket. How much money do you have?

This problem is pretty simple, but you may have used some advanced algebraic thinking as you solved it. Did you go through the process of adding `25` five times to get the value of the quarters? Or did you think, “I know that `4` quarters is `$1.00`, so `5` quarters must be `$1.25`”?

Substituting one known value in for another, equivalent value in a problem is an example of algebraic reasoning. We can apply this method—informally known as the substitution methodA method of solving a system of equations by substituting one quantity in for an equivalent quantity.—to solving systems of equationsA set of two or more equations that share two or more unknowns..

Adding up spare change is pretty simple. But complex problems also get easier using the substitution method—just look for quantities that are equal and then use those equivalences to speed up problem solving. Now put that `$1.50` back in your pocket and let’s get to work.

Using substitution to solve problems comes naturally to you. Take the following problem, for example:

Sean is `5` years older than four times his daughter’s age. His daughter is `7`. How old is Sean?

You can probably do this problem in your head. Sean’s daughter is `7`, so “four times his daughter’s age” is `28`, and `5` years on top of that is `33`. Sean is `33`.

If you solved the problem like that, you used a simple substitution—you substituted in the value “`7`” for “his daughter’s age.” You learned in the second part of the problem that “his daughter is `7`.” So substituting in a value of “`7`” for “his daughter’s age” in the first part of the problem was okay, because you knew these two quantities were equal.

Let’s try substitution in another, more abstract problem.

This problem looks different than the age one, but we can solve it in a similar way. We see from the first equation that `Omega=3`. Because `Omega` is equivalent to `3`, we can substitute `3` in every time we see `Omega` in the other equations, like this:

Now the second equation becomes easy to solve. If `3+Psi+Psi=27`, then `2Psi=24`, and `Psi=12`. Now we can substitute this value for `Psi`  into the last equation in order to find `Phi`: 

If `Phi+3 = 12`, then `Phi=9`. That’s it! We’ve found the values of all three symbols using only the substitution method.

Equivalence is the central idea in substitution problems. If we can find equivalent relationships within a system, we can use those relationships to solve the system.

In both problems above, an obvious equivalent relationship was presented within the scenarios: we were told straight out that the daughter’s age was `7` and the value of `Omega` was `3`. It wasn’t hard for us to use those equivalent relationships as convenient starting points for solving the systems. What do we do, though, in cases where equivalent relationships are not as obvious? Here’s one now:

In order to sell more of its produce, a local farm sells bags of apples in two sizes: medium and large. A medium bag contains `4` Macintosh and `1` Red Delicious apples and costs `$2.80`. A large bag contains `8` Macintosh and `4` Red Delicious apples and costs `$7.20`. How much does each kind of apple cost?

Let’s start by creating a system of equations that represents the two relationships in this problem, the cost of each kind of apple in the two different bags. We’ll use “`m`” to represent the cost of a Macintosh apple, and “`r`” will stand for the cost of a Red Delicious. Let’s make a table and see what we know and don’t know about our system:

Looking at these equations, there is no obvious equivalence—both equations have two variables. But wait—notice that the coefficient of `r` is `1` in the first equation? We can use what we know about manipulating algebraic equations to rewrite that equation in terms of `r`:

Now we have an equivalent value for `r`, one we can substitute for `r` in the second equation. Once we do that, we can solve that second equation for `m`.

Okay, we figured out that `m = 0.5`, so we can go back and substitute that into the first equation to find a value for `r`.

There we have it—the cost of one Macintosh apple is `50¢`, and the cost of one Red Delicious apple is `80¢`.

Notice that in the solution above, we solved the first equation for the variable `r` and used that equivalence to “unlock” the rest of the system. There is nothing magical about why we solved for `r`. We could have used any of the variables in the problem and arrived at the same result. Another path we could have taken is to have rewritten the first equation in terms of `4m`, and then substituted that equivalent relationship (`4m = 2.80-r`) into the second equation like this:

Solving this equation for `r` will yield the same value as in the previous solution method.

There are some cases where using the substitution method will yield results that, at first, do not make sense. Let’s take a look at some of these and figure out what is going on.

Solve for `x` and `y`.

`y = 5x + 4`

`10x-2y = 4`

Since the first equation is `y = 5x + 4`, we can substitute `5x + 4` in for `y` in the second equation.

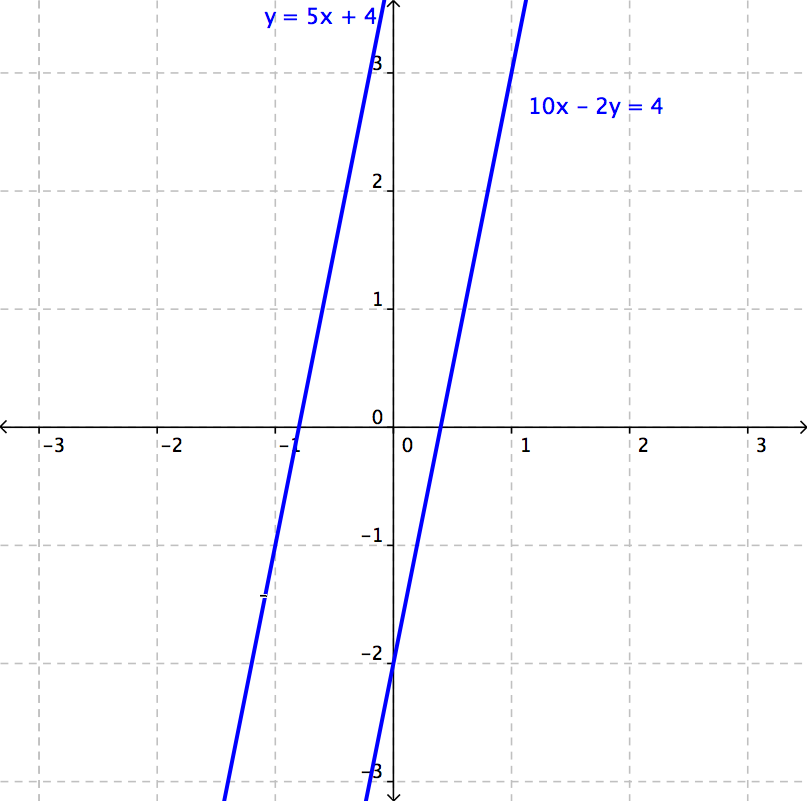
This doesn’t make sense. How can `0 = -4`? The graph of this system sheds some light on what is happening:

The reason we got a nonsensical answer is because the lines are parallel. If they never intersect, there will never be one point that is a solution to both equations. This system has no solutions.

Now take this problem, which has an interesting solution as well.

Solve for `x` and `y`.

`y = -0.5x`

`9y = -4.5x`

Substituting `-0.5x` in for `y` in the second equation, we find the following:

This time we get a true statement: `-4.5x = -4.5x`. But what does this type of answer mean? Again, graphing can help us make sense of this system:

This system consists of two equations for the same line. Every point along the line will be a solution to the system, and that’s why the substitution method yields a true statement. In this case, we say that there are an infinite number of solutions.

The substitution method is one way of solving systems of equations. To use the substitution method, first identify equivalent relationships within the system and then substitute these values into each equation in place of the variables. Solving using the substitution method will yield one of three possible results: a single value for each variable within the system (indicating one solution), an untrue statement (indicating no solutions), or a true statement (indicating infinite solutions).