Solving and Graphing Absolute Value Inequalities

Learning Objectives

• Solve absolute value inequalities in one variable using the Properties of Inequality.
• Represent absolute value inequalities on a number line.

The absolute valueThe value of a number without regard to its sign. of a value or expression describes its distance from `0`, but it strips out information on the sign of the number or the direction of the distance. Absolute value is always positive or zero, and a positive absolute value could result from either a positive or a negative original value.

When solving and graphing absolute value inequalitiesA math sentence that defines a range of numbers; inequalities contain the symbols `<`, `<=`, `>`, or `>=`., we have to consider both the behavior of absolute value and the Properties of InequalityA set of rules for inequalities that describe how addition, subtraction, multiplication, or division can be applied to both sides of an inequality in order to produce an equivalent inequality.. These types of inequalities behave in interesting ways—let’s get started.

We know that the absolute value of a number is a measure of size but not direction. So, for example, `|27|` and `|-27|` are both `27`—absolute value indicates the distance from `0`, but doesn’t bother with the direction.

Watching a weather report on the news, we may hear “Today’s high was `72^@`, but we’ll have a `10^@` swing in the temperature tomorrow. I’ll let you know which way we’re going after these commercials.” Based on this information, tomorrow’s high could be either `62^@` or `82^@`. The weatherman has said the difference between the temperatures, but he has not revealed in which direction the weather will go.

Finding the absolute value of signed numbers is pretty straightforward—just drop any negative sign.

Consider `|m|=7.5`, for instance. We know the absolute value of `m`, but the original value could be either positive or negative. So in this case we say that `m = 7.5` or `-7.5`. The graph below shows `|m| = 7.5` mapped on the number line. Notice that we’ve plotted both possible solutions.

Once the equal sign is replaced by an inequality, graphing absolute values changes a bit. Let’s stick with the example from above, ` |m| = 7.5`, but change the sign from `=` to `<=`. Now we have an absolute value inequality: `|m| <=7.5`. 

Think about this weather report: “Today at noon it was only `0^@`, and the temperature has changed at most `7.5^@` since then.” Notice this does not say which way the temperature moved, and it does not say exactly how much it changed—it just says that, at most, the temperature has changed `7.5^@`. We can represent this idea with the statement `|text(change in temperature)|<=7.5^@`.

To find out the full range of `m` values that satisfy this inequality, we need to evaluate both possibilities for `|m|`: `m` could be positive or `m` could be negative. If `m` is positive, then ` |m|` and `m` are the same number. If `m` is negative, then ` |m|` is the opposite of `m`, that is, ` |m|` is `-m`. So in this case we have two possibilities, `m<=7.5` and `-m<=7.5`. We need to solve for both:

It’s important to remember something here: when you multiply both sides of an inequality by a negative number, like we just did to turn `-m` into `m`, the inequality sign flips. If you forget to do that, you’ll be in trouble.

So `m` could be less than or equal to `7.5`, or greater than or equal to `-7.5`. Notice that the range of solutions includes both points (`-7.5` and `7.5`) as well as all points in between. Here is a graph of the inequality on a number line:

We could say "`m` is greater than or equal to `-7.5` and less than or equal to `7.5`." If `m` is any point between `-7.5` and `7.5` inclusive on the number line, then the inequality ` |m|<=7.5` will be true. We can write this as `-7.5<=m<=7.5`. This notation places the value of `m` between those two numbers, just as it is on the number line.

Let’s look at a different sort of situation. We’ll evaluate the absolute value inequality ` |g|>4`. 

We find that `g` could be greater than `4` or less than `-4`. If we map both those possibilities on a number line, it looks like this:

The graph shows one rayA half-line beginning at one point and continuing to infinity. (a half-line beginning at one point and continuing to infinity) beginning at `-4` and going to negative infinity, and another ray beginning at `+4` and going to infinity. We could say "`g` is less than `-4` or greater than `4`." That can be written algebraically as `-4>g>4`. This notation tells us that the value of `g` could be anything except what is between those numbers.

Notice the difference between this graph and the graph of ` |m|<=7.5`. In ` |m|<=7.5`, the range of possibilities that satisfied the inequality are the two points (`-7.5` and `7.5`) as well as everything that lies between them. In ` |g|>4`, however, the range of possible solutions lies outside the points, and extends to infinity in both directions.

A quick way to identify whether the absolute value inequality will be graphed as a segment between two points or as two rays going in opposite directions is to look at the direction of the inequality sign in relation to the variable.

For example, think about the inequality ` |x|<=2`, which could be modeled by someone walking a dog on a two-foot long leash. The dog can pull ahead up to the entire length of the leash, or lag behind until the leash tugs him along. He cannot be farther away from the person than two feet in either direction. In other words, the dog can only be at a distance less than or equal to the length of the leash. In the language of algebra, the location of the dog can be described by the inequality `-2<=x<=2`. The constant is the maximum value, and the graph of this will be a segment between two points.

Now consider the opposite inequality,` |x|>=2`. Imagine a high school senior who wants to go to college two hours or more away from home. He may choose a school three hours east, or five hours west—he’ll go anywhere, as long as it is at least `2` hours away. There is no upper limit to how far he will go. In mathematical terms, the situation can be written as the inequality `-2>=x>=2`. The constant is the minimum value, and the graph of this situation will be two rays that head out to negative and positive infinity and exclude every value within `2` of the origin.

The same Properties of Inequality apply when solving an absolute value inequality as when solving a regular inequality. The main difference is that in an absolute value inequality, you need to evaluate the inequality twice to account for both the positive and negative possibilities for the variable.

Let’s start with a one-step example: `3|h| <21`. The first step is to isolate the absolute value term on one side of the inequality. We can do that by dividing both sides by `3`, just as we would do in a regular inequality.

With the inequality in a simpler form, we can evaluate the absolute value as `h<7` and `h> -7`. The range of possible solutions for the inequality `3|h|<21` is all numbers from `-7` to `7` (not including `-7` and `7`).

How about a case where there is more than one term within the absolute value, as in the inequality: ` |p + 8|>5`? Let’s solve this one, too.

This means that the graph of the inequality will be two rays going in opposite directions, as shown below.

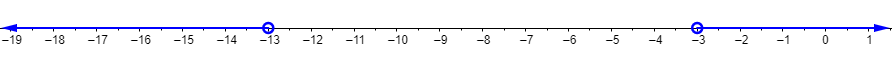
Let’s look at one more example: `56>=7|5-b|`. Since the absolute value term is less than the constant term, we are expecting the solution to be of the “and” sort: a segment between two points on the number line.

We find that `b>=-3` and `b<=13`, so any point that lies between `-3` and `13` (including those points) will be a solution to this problem.

An inequality defines a range of possible values for a mathematical relationship. The range for an absolute value inequality is defined by two possibilities—the original variable may be positive or it may be negative. This is why we have to evaluate it twice, once as a positive term, and once as a negative term.

The graph of the solution set of an absolute value inequality will either be a segment between two points on the number line, or two rays going in opposite directions from two points on the number line. Any point along the segment or along the rays will satisfy the original inequality.