Intercepts of Linear Equations

Learning Objectives

• Calculate the intercepts of a line.
• Use the intercepts to plot a line.

The interceptsA point where a line meets or crosses a coordinate axis. of a line are the points where the line intercepts, or crosses, the horizontal and vertical axes.

The straight line on the graph below intercepts the two coordinate axes. The point where the line crosses the `x`-axis is called the `x`-intercept. The `y`-intercept is the point where the line crosses the `y`-axis.

Notice that the `y`-intercept occurs where `x = 0`, and the `x`-intercept occurs where `y=0`.

We can use the characteristics of intercepts to quickly calculate them from the equation of a line. Just see how easy it is, as we find the `x`- and `y`-intercepts for the line `3y+2x=6`.

To find the `y`-intercept, we substitute `0` for `x` in the equation, because we know that every point on the `y`-axis has an `x`-coordinate of `0`. Once we do that, we can solve to find the value of `y`. When we make `x = 0`, the equation becomes `3y+2(0)=6`, which works out to `y = 2`. So when `x=0`, `y = 2`. The coordinates of the `y`-intercept are `(0,2)`.

Now we’ll follow the same steps to find the `x`-intercept. We’ll let `y = 0` in the equation, and solve for `x`. When `y = 0`, the equation for the line becomes `3(0)+2x=6`, and that works out to `x = 3`. When `y=0`, `x = 3`. The coordinates of the `x`-intercept are `(3,0)`.

See, I told you that it would be easy.

Knowing the intercepts of a line is useful. For one thing, it makes it easy to draw the graph of a line—we just have to plot the intercepts and then draw a line through them. Let’s do it with the equation `3y+2x=6`. We figured out that the intercepts of the line this equation represents are `(0, 2)` and `(3, 0)`. That’s all we need to know:

And there we have the line.

Intercepts are also valuable tools for predicting or tracking a process. At each intercept, one of the two quantities being plotted reaches zero. That means that the intercepts of a line can be used to mark the beginning and the end of a process.

Imagine a student named Morgan who is buying a laptop for `$1,080` to use for school. Morgan is going to use the computer store’s finance plan to make this purchase—she’ll pay `$45` per month for `24` months.

She wants to know how much she will still owe after each month of the plan. She can keep track of her debt by making a graph. The `x`-axis will be the number of months and the `y`-axis will represent the amount of money she still owes on the finance plan. Morgan knows two points in her pay-off schedule. The day she buys the computer, she’ll be at `0` months passed and `$1,080` owed. The day she pays it off completely, she’ll be at `24` months passed and `$0` owed. With these two points, she can draw a line, running from the `y`-intercept at `(0, 1080)` to the `x`-intercept at `(24,0)`.

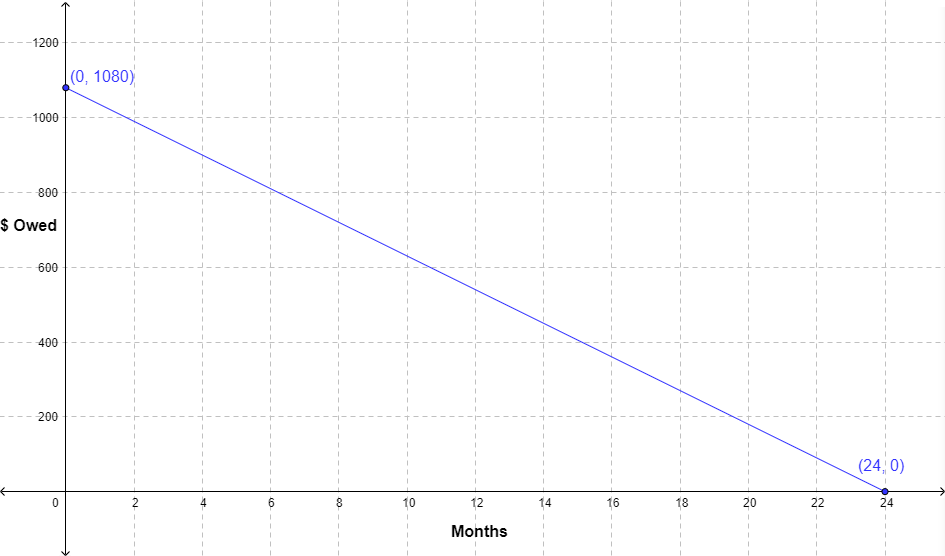
Morgan can now use this graph to figure out how much money she still owes after any number of months.

Let’s look at another situation involving intercepts, this time when we know only one intercept and want to find the other. Joe is a lifeguard at the local swimming pool. It’s the end of the summer, and the pool is being drained. Joe has to wait by the pool until it’s completely empty, so no one falls in and drowns. How can poor Joe figure out how long that’s going to take?

If Joe has taken an algebra course, he’s got it made. The pool contains `10,200` gallons of water. It drains at a rate of `680` gallons per hour. Joe can use that information to make a table of how much water will be left in the pool hour by hour.

Once he’s calculated a few data points, Joe can use a graph and intercepts as a short-cut to find out how long it will be until the pool is dry. Joe’s starting point is the `y`-intercept, where the pool is full at `10,200` gallons and the elapsed time is `0`. Next, he plots the volume of the pool at `1`, `2`, `3`, and finally `4` hours.

Now all Joe needs to do is connect the points with a line, and then extend the line until it meets the `x`-axis.

The line intercepts the `x`-axis when `x = 15`. So now Joe knows—the pool will take `15` hours to drain completely. It’s going to be a long day.

We’ve now seen the usefulness of the intercepts of a line. When we know where a line crosses the `x`- and `y`-axes, we can easily produce the graph or the equation for that line. When we know one of the intercepts and the slope of a line, we can find the beginning or predict the end of a process.