| absolute value | the value of a number without regard to its sign |
| Addition Property of Equality | allows us to add the same amount to both sides of an equation: For all real numbers a, b, and c, if a = b, then a + c = b + c |
| Addition Property of Identity | states that any number plus zero equals that number: For all real numbers a, a + 0 = a |
| Additive Inverse Property | states that every real number added to its additive inverse (or opposite) will equal zero: For all real numbers a, a + (-a) = 0; also called Inverse Property of Addition |
| algebra | the branch of mathematics that deals with operations on sets of numbers and relationships between them |
| area model | a graphic representation of a multiplication problem, in which the length and width of a rectangle are the factors and the area is the product |
| Associative Property of Addition | states that numbers in an addition sequence can be added in any order, and the value of the expression will not change: For all real numbers a, b, and c, (a + b) + c = a + (b + c) |
| Associative Property of Multiplication | states that numbers in a multiplication sequence can be multiplied in any order, and the value of the expression will not change: For all real numbers a, b, and c, (ab)c = a(bc) |
| axis of symmetry | a line of symmetry for a graph—it divides a figure or graph into halves that are the mirror images of each other |
| base | the value that is raised to a power when a number is written in exponential notation. In the term 53, 5 is the base and 3 is the exponent. |
| binomial | a sum of two monomials, such as 3x2 + 7 |
| boundary line | a line that represents the edge of a linear inequality: if points along the boundary line are included in the solution set, then a solid line is used; if points along the boundary line are not included in the solution set, then a dashed line is used |
| bounded region | the set of solutions that are true for all of the linear inequalities under consideration |
| coefficient | a number that multiplies a variable |
| combinations | groupings in which the order of members does not matter |
| common denominator | a number that is a multiple of all of the denominators in a group of fractions |
| Commutative Property of Addition | states that when two values are added together, changing their order does not affect their sum: For all real numbers a and b, a + b = b + a |
| Commutative Property of Multiplication | states that when two values are multiplied together, changing their order does not affect their product: For all real numbers a and b, ab = ba |
| completing the square | |
| compound event | an event with more than one outcome |
| conclusion | the part of a logical statement that provides the result or consequences of the hypothesis—In a statement “If x then y”, the conclusion is y. |
| conjecture | a statement that attempts to make a conclusion but has not been proved true or false |
| constant of proportionality | the constant in a proportional function equation; it describes the ratio or proportional relationship of the independent and dependent variables—also called the constant of variation or the rate of change |
| constant of variation | the constant in a proportional function equation; it describes the ratio or proportional relationship of the independent and dependent variables—also called the rate of change or the constant of proportionality |
| continuous pattern | a pattern made of uninterrupted or connected values or objects |
| coordinate plane | a plane in two dimensions, containing the x- and y-axes, used to map ordered pairs in the form (x, y) |
| coordinates | a pair of numbers that identifies a point on the coordinate plane—the first number is the x-value and the second is the y-value |
| counterexample | a situation that provides evidence that a logical statement is false |
| counting numbers | also called natural numbers, the numbers 1, 2, 3, 4, ... |
| deductive reasoning | a form of logical thinking that uses generalizations to draw specific conclusions based on a series of logical steps, deductive reasoning may use rules, laws, and theories to support or justify a conjecture |
| dependent events | two or more events for which the occurrence of one affects the probability of the other(s) |
| dependent value | a value or variable that depends upon the independent value |
| dependent variable | a value or variable that depends upon the independent value |
| discrete pattern | a pattern made of separate and distinct values or objects |
| discrete values | values that change in increments (not continuously) |
| discriminant | the expression b2 – 4ac under the radical in the quadratic formula; the expression can be used to determine the number of real roots the quadratic equation has |
| Distributive Property | states that the product of a number and a sum equals the sum of the individual products of the number and the addends: for all real numbers a, b, and c, a(b + c) = ab + ac |
| Division Property of Equality | allows us to divide both sides of an equation by the same amount: For all real numbers a, b, and c, if a = b and c is not 0, then  |
| domain | the set of all possible inputs of a function which allow the function to work |
| elimination method | a method of solving a system of equations by adding or subtracting equations in order to eliminate a common variable |
| equally likely | having the same likelihood of occurring, such that in a large number of trials, two equally likely outcomes would happen roughly the same number of times |
| equation | a statement that describes the equality of two expressions by connecting them with an equals sign |
| event | a collection of possible outcomes, often describable using a common characteristic, such as rolling an even number with a die or picking a card from a specific suit |
| event space | the set of possible outcomes in an event: for example, the event “rolling an even number” on a die has the event space of 2, 4, and 6 |
| example | a situation that suggests a logical statement may be true |
| excluded value | a value for a variable that is not allowed in an expression, such as a variable in a rational expression that would make the denominator equal zero |
| exponent | the value that indicates the number of times another value is multiplied by itself in exponential notation. The exponent, also called the power, is written in superscript. In the term 53, 5 is the base and 3 is the exponent. |
| exponential function | a nonlinear function in which the independent value is an exponent in the function, as in y = abx |
| exponential notation | a condensed way of expressing repeated multiplication of a value by itself. Exponential notation consists of a base and an exponent. In the exponential term 53, 5 is the base and 3 is the exponent. This is a shorthand way of writing 5 • 5 • 5. Also called exponential form. |
| extraneous solution | a solution that results from solving an equation that is not a valid solution in the original equation |
| factor | for any number x, the numbers that can be evenly divided into x are called factors of x. For example, the number 20 has the factors 1, 2, 4, 5, 10, and 20. |
| factored form of a polynomial | a polynomial written as a product of factors, and each non-monomial factor has no common factors in its terms |
| factorial | an abbreviated way of writing a product of all whole numbers from 1 to a given number, indicated by that number followed by an exclamation point, as in 3! = 3 • 2 • 1 |
| factoring | the process of breaking a number down into its multiplicative factors. Every number x has at least the numbers 1 and x as factors. |
| formula | a type of equation—usually reserved for multi-variable equations that describe a well-known or often repeated calculation |
| function | a kind of relation in which one variable uniquely determines the value of another variable |
| Fundamental Counting Principle | a way to find the number of outcomes in a sample space by finding the product of the number of outcomes for each element |
| generalize | the process of using observations of specific events to make statements or conjectures about more general situations |
| greatest common factor | the largest number or expression that will divide a number or expression exactly |
| greatest common factor (GCF) | the largest factor that two numbers have in common |
| grouping technique | a factoring technique involving finding common factors among groups of terms rather than among all of terms |
| half-plane | on a coordinate plane, the shape of the region of possible solutions generated by a single inequality |
| hypotenuse | the side opposite the right angle in any right triangle—the hypotenuse is the longest side in a right triangle |
| hypothesis | the part of a logical statement that provides the premise on which the conclusion is based—In a statement “If x then y,” the hypothesis is x. |
| independent events | two or more events for which the occurrence of one does not affect the probability of the other(s) |
| independent value | a value or variable that changes or can be manipulated by circumstances |
| independent variable | a value or variable that changes or can be manipulated by circumstances |
| inductive reasoning | a form of logical thinking that makes general conclusions based on specific situations, inductive reasoning takes the path of observation to generalization to conjecture |
| inequality | a math sentence that defines a range of numbers; inequalities contain the symbols <, ≤, >, or ≥ |
| input | the independent variable of a function—input determines output |
| integers | the numbers …, -3, -2, -1, 0, 1, 2, 3,… |
| intercept | a point where a line meets or crosses a coordinate axis |
| intercept form of a quadratic equation | written as y = a(x – p)(x – q), where the x-intercepts are p and q |
| inverse function | a nonlinear function in which the reciprocal of the independent variable times a constant equals the dependent variable, as in  |
| Inverse Operations | operations that undo or cancel one another, such as addition/subtraction and multiplication/division |
| Inverse Property of Addition | states that every real number added to its additive inverse (or opposite) will equal zero: for all real numbers a, a + (-a) = 0; also called Additive Inverse Property |
| Inverse Property of Multiplication | states that any number multiplied by 1 over that number equals 1: For all real numbers a,  ; also called Multiplicative Inverse Property ; also called Multiplicative Inverse Property |
| irrational numbers | numbers between integers that cannot be written as a ratio of integers (that is, as  where p and q are both integers), the decimal representation of an irrational number is non-repeating and non-terminating where p and q are both integers), the decimal representation of an irrational number is non-repeating and non-terminating |
| justify | provide a logical argument for a conclusion or conjecture |
| least common denominator | the smallest number or expression that is a multiple of all the denominators in a group of fractions or rational expressions |
| least common multiple | the smallest number or expression that is a multiple of a group of numbers or expressions |
| leg | in a right triangle, one of the two sides creating the right angle |
| like terms | two or more monomials that contain the same variables raised to the same powers, regardless of their coefficients. For example, 2x2y and -8x2y are like terms because they have the same variables raised to the same exponents. |
| linear equation | an equation that describes a straight line |
| linear function | a function with a constant rate of change and a straight line graph |
| linear inequality | an inequality represented in a form equivalent to Ax + By > C, where the symbol > could also be <, ≤, or ≥ |
| logical argument | a series of statements, each verifiable as true, that lead to a conclusion |
| logical statement | a statement that allows drawing a conclusion or result based on a hypothesis or premise |
| mathematical sequence | an ordered list of numbers or objects |
| monomial | a number, a variable, or a product of a number and one or more variables with whole number exponents, such as -5, x, and 8xy3 |
| multi-step equation | an equation that requires more than one step to solve |
| Multiplication Property of Equality | allows us to multiply both sides of an equation by the same amount: For all real numbers a, b, and c, if a = b, then ac = bc |
| Multiplication Property of Identity | states that any number times 1 equals that number: For all real numbers a, a • 1 = a |
| Multiplicative Inverse Property | states that any number multiplied by 1 over that number equals 1: For all real numbers a,  ; also called Inverse Property of Multiplication ; also called Inverse Property of Multiplication |
| natural numbers | also called counting numbers, the numbers 1, 2, 3, 4, … |
| nonlinear function | a function with a variable rate of change that graphs as a curved line |
| nonrepeating decimals | numbers whose decimal parts continue without repeating, these are irrational numbers |
| nonterminating decimals | numbers whose decimal parts continue (with non-zero digits) forever, these decimals can be rational (if they repeat) or irrational (if they are nonrepeating) |
| numeric constant | a quantity that has a known, fixed value |
| operation | a mathematical procedure, such as addition, subtraction, multiplication, and division |
| outcome | a result of a trial |
| output | the dependent variable of a function—output is determined by input |
| overgeneralize | a logical mistake caused by basing a generalization on inadequate evidence or observation or by making too broad a conjecture, such as generalizing a pattern seen only in whole numbers to all real numbers |
| parabola | a U-shaped graph which is produced by a quadratic equation |
| parallel lines | lines that have the same slope and different y-intercepts |
| partial products | a method of multiplication in which each factor is split into a sum of its parts. Every part of one factor is multiplied by every part of the other factor, then these partial products are added together. For example, (5)(23) = (5)(20 + 3) = 5(20) + 5(3) = 100 + 15 = 115 |
| perfect square | any of the squares of the integers. Since 12 = 1, 22 = 4, 32 = 9, etc., 1, 4, and 9 are perfect squares |
| perfect square trinomial | a trinomial that is the product of a binomial times itself, such as r2 + 2rs + s2 (from (r + s)2), and r2 – 2rs + s2 (from (r – s)2) |
| permutations | groupings in which the order of members matters |
| perpendicular lines | lines that have opposite reciprocal slopes |
| point-slope formula | a form of linear equation, written as , where m is the slope and (x1, y1) are the co-ordinates of a point , where m is the slope and (x1, y1) are the co-ordinates of a point |
| polynomial | a monomial or sum of monomials, like 4x2 + 3x – 10 |
| polynomial functions | a monomial or sum of monomials, like y = 4x2 + 3x – 10 |
| power | a way of describing the exponent in exponential notation. We can say the base is raised to the power of the exponent. For example we read x5 as “x raised to the 5th power.” |
| power of a power | raising a value written in exponential notation to a power as in (x2)3 |
| prime factor | a factor that has no factors but 1 and itself. For example, 2 is a prime factor of 12 because its only factors are 1 and 2, while 6 is not a prime factor of 12 because it has more factors than 1 and 6 (i.e. 2 and 3). |
| prime factorization | the process of breaking a number down into its prime factors |
| prime number | a whole number for which the only factors are 1 and the number itself |
| prime trinomial | a trinomial that cannot be factored using integers |
| probability | a measure of how likely it is that something will occur |
| product of powers | multiplication of two or more values in exponential form that have the same base—the base stays the same and the exponents are added |
| Properties of Inequality | a set of rules for inequalities that describe how addition, subtraction, multiplication, or division can be applied to both sides of an inequality in order to produce an equivalent inequality |
| Property of Equality | states that the equality of an equation is maintained when both sides have the same value added, subtracted, multiplied, or divided |
| proportional function | a function in which the input times a constant equals the output |
| Pythagoras | a Greek philosopher and mathematician who lived in the 6th Century BC |
| Pythagorean Theorem | the formula used to relate the lengths of the sides in any right triangle  |
| quadratic equation | an equation that can be written in the form ax2 + bx + c = 0 where a ¹ 0. When written as y = ax2 + bx + c the expression becomes a quadratic function. |
| quadratic formula | the formula  ; it is used to solve a quadratic equation of the form ; it is used to solve a quadratic equation of the form  |
| quadratic function | a function of the form y = ax2 + bx + c where a is not equal to zero |
| quotient of powers | division of two or more values in exponential form that have the same base—the base stays the same and the exponent in the denominator is subtracted from the exponent in the numerator |
| radical | the math symbol  , used to denote the process of taking a root of a quantity , used to denote the process of taking a root of a quantity |
| radical equation | an equation that contains a variable within a radical term |
| radical expression | a quantity that contains a term with a radical, as in  |
| radicand | the number under the radical symbol |
| raised to a power | a way of describing the exponent in exponential notation. We can say the base is “raised to the power” of the exponent. For example we read x5 as “x raised to the 5th power.” |
| random | unable to be predicted with certainty |
| range | the set of all possible outputs of a function |
| rate | a mathematical way of relating two quantities, which usually are measured in different units |
| rate of change | the constant in a proportional function equation; it describes the ratio or proportional relationship of the independent and dependent variables—also called the constant of variation or the constant of proportionality |
| rational equation | an equation that contains one or more rational expressions |
| rational expression | a fraction with a polynomial in the numerator and/or denominator |
| rational numbers | numbers that can be written as a ratio of integers (that is, as  where p and q are both integers and q ≠ 0) where p and q are both integers and q ≠ 0) |
| ray | a half-line beginning at one point and continuing to infinity |
| real numbers | the set of numbers that includes both rational numbers and irrational numbers. |
| reciprocal | |
| relation | the relationship between variables that change together |
| repeating decimals | numbers whose decimal parts repeat a pattern of one or more digits, these are all rational numbers |
| replacement | restoring a random situation back to its original state after performing an action |
| right triangle | a triangle with one right angle |
| rise | vertical change between two points |
| root | any number x multiplied by itself a specific number of times to produce another number, such that in xn = y, x is the nth root of y – for example, because 23 = 8, 2 is the 3rd (or cube) root of 8 |
| root of an equation | any number that makes the equation true when the variable is equal to that number. That is, a solution of the equation. |
| roots of a quadratic equation | the x-intercepts of the parabola or the solution of the equation |
| run | horizontal change between two points |
| sample space | the set of all outcomes |
| scientific notation | a convention for writing very large and very small numbers in which a number is expressed as the product of a power of 10 and a number that is greater than or equal to 1 and less than 10 as in 3.2 • 104 |
| simple event | an event with only one outcome |
| slope | the ratio of the vertical and horizontal changes between two points on a surface or a line |
| slope formula | the equation for the slope of a line, written as  , where m is the slope and (x1, y1) and (x2, y2) are the coordinates of two points on the line , where m is the slope and (x1, y1) and (x2, y2) are the coordinates of two points on the line |
| slope-intercept form | a linear equation, written in the form y = mx + b, where m is the slope and b is the y-intercept |
| slope-intercept formula | a linear equation, written as y = mx + b, where m is the slope and b is the y-intercept |
| special product | a product resulting from binomial multiplication that has certain characteristics. For example x2 – 25 is called a special product because both its terms are perfect squares and it can be factored into (x + 5)(x – 5). |
| standard form of a linear equation | a linear equation, written in the form Ax + By = C, where x and y are variables and A, B, and C are integers |
| standard form of a quadratic equation | written as  , where x and y are variables and a, b, and c are numbers with a ≠ 0. In the case of a single variable the standard form becomes ax2 + bx + c = 0. , where x and y are variables and a, b, and c are numbers with a ≠ 0. In the case of a single variable the standard form becomes ax2 + bx + c = 0. |
| substitution method | a method of solving a system of equations by substituting one quantity in for an equivalent quantity |
| Subtraction Property of Equality | allows us to subtract the same amount from both sides of an equation: For all real numbers a, b, and c, if a = b, then a – c = b – c |
| system of equations | a set of two or more equations that share two or more unknowns |
| system of inequalities | a set of two or more inequalities that must hold true at the same time |
| term | a value in a sequence--the first value in a sequence is the 1st term, the second value is the 2nd term, and so on; a term is also any of the monomials that make up a polynomial |
| terminating decimals | numbers whose decimal parts do not continue indefinitely but end eventually, these are all rational numbers |
| tree diagram | a diagram that shows the choices or random outcomes from multiple elements, using branches for each new element |
| trial | a random action or series of actions |
| trinomial | a three-term polynomial |
| variable | a symbol that represents an unknown value |
| vertex | the high point or low point of a parabolic function |
| vertex form of a quadratic equation | when the quadratic equation is a quadratic function, the vertex form is 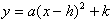 , where x and y are variables and a, h, and k are numbers – the vertex of this parabola has the coordinates (h, k) , where x and y are variables and a, h, and k are numbers – the vertex of this parabola has the coordinates (h, k) |
| whole numbers | the numbers 0, 1, 2, 3, …., or all natural numbers plus 0 |
| x-intercept | the point where a line meets or crosses the x-axis |
| y-intercept | the point where a line meets or crosses the y-axis |
| Zero Product Property | states that if ab = 0, then either a = 0 or b = 0, or both a and b are 0 |
![]() into a perfect square trinomial
into a perfect square trinomial ![]() , or
, or ![]()
![]()
![]()
![]() ; also called Multiplicative Inverse Property
; also called Multiplicative Inverse Property![]() where p and q are both integers), the decimal representation of an irrational number is non-repeating and non-terminating
where p and q are both integers), the decimal representation of an irrational number is non-repeating and non-terminating![]() ; also called Inverse Property of Multiplication
; also called Inverse Property of Multiplication![]() , where m is the slope and (x1, y1) are the co-ordinates of a point
, where m is the slope and (x1, y1) are the co-ordinates of a point![]()
![]() ; it is used to solve a quadratic equation of the form
; it is used to solve a quadratic equation of the form ![]()
![]() , used to denote the process of taking a root of a quantity
, used to denote the process of taking a root of a quantity![]()
![]() where p and q are both integers and q ≠ 0)
where p and q are both integers and q ≠ 0)![]() because
because ![]() ; the reciprocal of
; the reciprocal of ![]() is
is ![]() . It is also called the multiplicative inverse.
. It is also called the multiplicative inverse.![]() , where m is the slope and (x1, y1) and (x2, y2) are the coordinates of two points on the line
, where m is the slope and (x1, y1) and (x2, y2) are the coordinates of two points on the line![]() , where x and y are variables and a, b, and c are numbers with a ≠ 0. In the case of a single variable the standard form becomes ax2 + bx + c = 0.
, where x and y are variables and a, b, and c are numbers with a ≠ 0. In the case of a single variable the standard form becomes ax2 + bx + c = 0.![]() , where x and y are variables and a, h, and k are numbers – the vertex of this parabola has the coordinates (h, k)
, where x and y are variables and a, h, and k are numbers – the vertex of this parabola has the coordinates (h, k)