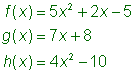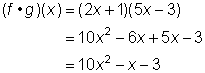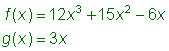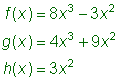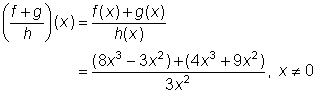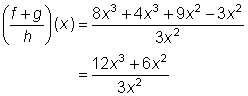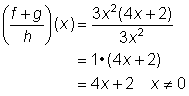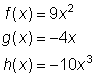Operaciones Aritméticas con Funciones

Operaciones aritméticas con funciones

Objetivos de aprendizaje

· Dadas dos funciones, f y g, encontrar su suma, f + g.

· Dadas dos funciones, f y g, encontrar su resta, f – g.

· Dadas dos funciones, f y g, encontrar su producto, f • g.

· Dadas dos funciones, f y g, encontrar su cociente, f/g.

Introducción

Estás acostumbrado a sumar, restar, multiplicar y dividir números reales, haces estas operaciones todos los días en una variedad de situaciones. También has aprendido cómo realizar estas cuatro operaciones básicas en expresiones algebraicas. Entonces, aunque no necesitas calcular muy a menudo, sabes cómo hacerlo.

Si sabes cómo realizar las cuatro operaciones básicas en polinomios, entonces también puedes sumar, restar, multiplicar y dividir funciones. La notación se verá diferente al principio, pero aprender un par de pasos te puede ayudar a llegar a la respuesta correcta.

Entendiendo la notación

Una función es una correspondencia entre dos conjuntos: el dominio y el rango. Además de evaluar funciones, puedes hacer operaciones con funciones.

Digamos que trabajas con las siguientes dos funciones.

La suma de las funciones puede escribirse como f(x) + g(x) o (f + g)(x). Observa lo que sucede cuando se suman estas dos funciones.

Y es todo, la suma de las dos funciones es la suma de los dos polinomios.

La suma, la resta, la multiplicación y la división se explicarán también. La tabla siguiente muestra la notación usada para cada tipo de operación aritmética.

Suma
Resta
Multiplicación
División

Sumando y restando

Ya viste un ejemplo de sumar dos funciones. Veamos otro ejemplo. El dominio (los valores de x) para ambas funciones es todos los números reales.

Ejemplo
Problema	*Encontrar (f + g)(x).*
		Identifica f(x) y g(x). Reemplaza f(x) con y g(x) con . Luego suma y combina los términos semejantes.
Respuesta

La resta sigue el mismo proceso. Siempre y cuando te acuerdes de cómo restar un polinomio de otro, puedes restar una función de otra.

Ejemplo
Problema	Encontrar (g – f)(x).
		Reemplaza g(x) y f(x) con sus respectivas expresiones. Luego suma y combina los términos semejantes.
Respuesta

Ejemplo
Problema	*Encontrar (f – h)(x).*
		Observa que (f – h)(x) = f(x) – h(x). Puedes ignorar g(x) porque no se requiere resolver para este problema. Reemplaza las notaciones de función con sus polinomios apropiados y resta.
Respuesta

y . ¿Qué es

Mostrar/Ocultar Respuesta

Multiplicando y dividiendo

Multiplicar y dividir funciones también es como multiplicar y dividir polinomios. Revisa los siguientes ejemplos.

Ejemplo
Problema	Encontrar el producto de f y g.
		Para encontrar el producto, multiplica las funciones.
		Reemplaza f(x) con (2x + 1) y g(x) con (5x – 3).
Respuesta

Ejemplo
Problema	Encontrar .
		Para encontrar el cociente, divide f entre g. Sustituye los polinomios por f(x) y g(x) y divide. Sumamos porque x = 0 haría el denominador g(x) =0 y indefinida. Recuerda renombrar como 1.
Respuesta

Las operaciones con tres funciones trabajan de la misma forma. En el ejemplo siguiente, dos funciones se suman y luego se dividen entre una tercera función. No es distinto de lo que ya has hecho con polinomios, sólo no dejes de sustituir los polinomios en las funciones correctas, combina, divide y simplifica.

Ejemplo
Problema	Encontrar .
		Reemplaza f(x), g(x) y h(x) con polinomios equivalentes. Sumamos porque eso haría 0 el denominador h(x) de y la fracción no estaría definida.
		Suma f(x) y g(x).
		Divide entre h(x). Saca el factor de 3x² del numerador y luego simplifica la expresión, usando .
Respuesta

Encontrar .

Mostrar/Ocultar Respuesta

Sumario

Así como los enteros y las expresiones algebraicas, las funciones pueden sumarse, restarse, multiplicarse y dividirse. Para realizar una operación aritmética de dos o más funciones, reemplaza la función indicada con su polinomio respectivo, luego combina usando las reglas normales de la suma, la resta, la multiplicación y la división.