Multiplicando y dividiendo expresiones radicales
Objetivos de aprendizaje
· Multiplicar y simplificar expresiones radicales que contienen un sólo término.
· Dividir y simplificar expresiones radicales que contienen un sólo término.
Introducción
Puedes hacer más que sólo simplificar expresiones radicales. También puedes multiplicarlas y dividirlas. Puedes aplicar tu conocimiento de los exponentes para ayudarte cuando tienes que operar expresiones radicales.
Empecemos con una cantidad que ya has visto antes, ![]() . Puedes simplificar esta raíz cuadrada pensando en ella como
. Puedes simplificar esta raíz cuadrada pensando en ella como ![]() .
.
|
|
Si piensas en el radicando como un producto de dos factores (aquí, pensando en el 64 como el producto de 16 y 4), puedes obtener la raíz cuadrada de cada factor y luego multiplicar las raíces. El resultado final es el mismo, ![]() .
.
Este es un ejemplo de la regla del producto elevado a una potencia. Esta regla dice que el producto de dos o más números elevados a una potencia es igual al producto de cada número elevado a la misma potencia.
Esta debe ser una idea familiar. Aplicas esta regla cuando expandes expresiones como (ab)x a ax • bx; ahora vas a modificarla para incluir también a los radicales. Imagina que el exponente x no es un entero sino una fracción unitaria, como ![]() , por lo que tienes la expresión
, por lo que tienes la expresión ![]() . De acuerdo con la regla del producto elevado a una potencia
. De acuerdo con la regla del producto elevado a una potencia ![]() , que es lo mismo que
, que es lo mismo que ![]() , porque los exponentes fraccionales pueden escribirse como raíces. Entonces, por la misma razón que
, porque los exponentes fraccionales pueden escribirse como raíces. Entonces, por la misma razón que ![]() , tenemos que
, tenemos que ![]() .
.
Regla del producto elevado a una potencia
Para cualesquiera números a y b y cualquier entero x:
Para cualesquiera números a y b y cualquier entero positivo x:
Para cualesquiera números a y b y cualquier entero positivo x:
|
La regla del producto elevado a una potencia es importante porque puedes usarla para multiplicar expresiones racionales. Observa que las raíces son iguales, por ejemplo, puedes combinar raíces cuadradas con raíces cuadradas, o raíces cúbicas con raíces cúbicas. Pero no puedes multiplicar una raíz cuadrada con una raíz cúbica usando esta regla.
Veamos otro ejemplo.
| Ejemplo | ||
| Problema | Simplificar. | |
|
|
| Usa la regla |
|
|
|
|
|
|
| Busca cuadrados perfectos en el radicando y reescribe el radicando como el producto de dos factores. |
|
|
| Identifica los cuadrados perfectos. |
|
|
| Reescribe como el producto de dos radicandos. |
|
|
| Simplifica, usando |
| Respuesta |
|
|
Usando la regla del producto elevado a una potencia, puedes tomar una expresión complicada, ![]() y convertirla en algo más manejable,
y convertirla en algo más manejable, ![]() .
.
También habrás notado que ![]() y
y ![]() pueden escribirse como productos con factores cuadrados perfectos. ¿Cómo cambiaría la expresión si primero simplificas cada radical, antes de multiplicar?
pueden escribirse como productos con factores cuadrados perfectos. ¿Cómo cambiaría la expresión si primero simplificas cada radical, antes de multiplicar?
| Ejemplo | ||
| Problema | Simplificar. |
|
|
|
| Busca cuadrados perfectos en el radicando y reescribe el radicando como el producto de dos factores. |
|
|
| Identifica los cuadrados perfectos. |
|
|
| Reescribe como el producto de dos radicandos. |
|
|
| Simplifica, usando |
|
|
| Multiplica. |
| Respuesta |
|
|
En ambos casos, llegas al mismo producto, ![]() . No importa si primero multiplicas los radicandos o simplificas cada radicando.
. No importa si primero multiplicas los radicandos o simplificas cada radicando.
Multiplicas expresiones radicales que contienen variables de la misma manera. Siempre y cuando las raíces de las expresiones radicales sean iguales, puedes usar la regla del producto elevado a una potencia para multiplicar y simplificar. Observa los siguientes dos ejemplos. En ambos problemas, primero se usa la regla del producto elevado a una potencia y luego se simplifica la expresión.
| Ejemplo | ||
| Problema | Simplificar. | |
|
|
| Usa la regla |
|
|
|
|
|
|
| Recuerda que |
|
|
|
|
|
|
| Busca cuadrados perfectos en el radicando. |
|
|
| Reescribe como el producto de radicales. |
|
|
|
|
| Respuesta |
|
|
| Ejemplo | ||
| Problema | Simplificar. |
|
|
|
| Observa que ambos radicales son raíces cúbicas, por lo que puedes usar la regla |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Busca cuadrados perfectos en el radicando. Como |
|
|
| Reescribe como el producto de radicales. |
|
|
|
|
| Respuesta |
|
|
El siguiente ejemplo es un poco más complicado porque hay más de dos radicales siendo multiplicados. En este caso, observa cómo los radicales se simplifican antes de multiplicar. (Recuerda que el orden que sigas depende de ti, a veces es más fácil multiplicar antes de simplificar, otras veces es más fácil simplificar antes de multiplicar. Con algo de práctica, serás capaz de identificar qué método usar para cada problema, pero cualquier orden funciona para todos los problemas.)
| Ejemplo | ||
| Problema | Simplificar. | |
|
|
| Observa que esta expresión está multiplicando tres radicales con la misma raíz. Simplifica cada radical, si es posible, antes de multiplicar. Busca potencias de 4 en cada radicando. |
|
|
| Reescribe como el producto de radicales. |
|
|
| Identifica y saca las potencias de 4, usando el hecho de que |
|
|
| Como todos los radicales son raíces cuartas, puedes usar la regla |
|
|
|
|
|
|
| Ahora que los radicandos han sido multiplicados, busca de nuevo potencias de 4 y sácalas. Podemos olvidarnos de los signos de valor absolutos en la respuesta final porque al inicio del problema nos dijeron que |
| Respuesta |
|
|
| ¿Cuál de las siguientes pares de problema y respuesta es incorrecto?
A) Problema: B) Problema: C) Problema: D) Problema:
|
Puedes usar las mismas ideas para encontrar la forma de simplificar y dividir expresiones radicales. Recuerda que la regla del producto elevado a una potencia dice que ![]() . Entonces, ¿qué si estamos tratando con un cociente en lugar de un producto?
. Entonces, ¿qué si estamos tratando con un cociente en lugar de un producto?
También hay una regla para eso. La regla del cociente elevado a una potencia dice que ![]() . De nuevo, si imaginas que el exponente es un número racional, entonces puedes hacer aplicable esta regla también para raíces:
. De nuevo, si imaginas que el exponente es un número racional, entonces puedes hacer aplicable esta regla también para raíces: 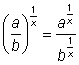 , entonces
, entonces ![]() .
.
Regla del cociente elevado a una potencia
Para cualesquiera números a y b (b ≠ 0) y cualquier entero positivo x:
Para cualesquiera números a y b(b ≠ 0) y cualquier entero positivo x:
|
Del mismo modo que con la multiplicación, empezarás con algunos ejemplo con enteros antes de pasar a expresiones más complejas como 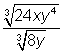 .
.
| Ejemplo | ||
| Problema | Simplificar. |
|
|
|
| Usa la regla |
|
|
| Simplifica cada radical. Busca factores cuadrados perfectos en el radicando y reescríbelo como el producto de factores. |
|
|
| Identifica y saca los cuadrados perfectos. |
|
|
|
|
|
|
| Simplifica. |
| Respuesta |
|
|
| Ejemplo | ||
| Problema | Simplificar. |
|
|
|
| Reescribe usando la regla del cociente elevado a una potencia. |
|
|
| Simplifica cada radical. Busca factores cuadrados perfectos en el radicando y reescríbelo como el producto de factores. |
|
|
| Identifica y saca los cuadrados perfectos. |
|
|
|
|
|
|
|
|
|
|
| Puedes simplificar esta expresión aún más buscando factores comunes en el numerador y en el denominador. |
|
|
| Reescribe el numerador como un producto de factores. |
|
|
| Identifica factores de 1 y simplifica. |
| Respuesta |
|
|
Eso fue mucho esfuerzo, pero pudiste simplificar usando la regla del cociente elevado a una potencia. ¿Qué si hubieras encontrado el cociente de esta expresión dividiendo primero en el radical y luego encontrar la raíz cúbica del cociente?
Veamos otro problema.
| Ejemplo | ||
| Problema | Simplificar. |
|
|
|
| Como ambos radicales son raíces cúbicas, puedes usar la regla |
|
|
| Dentro del radical, divide 640 entre 40. |
|
|
| Busca cubos perfectos en el radicando y reescríbelo como el producto de factores. |
|
|
| Identifica los cubos perfectos y sácalos. |
|
|
|
|
|
|
| Simplifica. |
| Respuesta |
|
|
Ese fue un método más directo, ¿no?
De la misma forma que con la multiplicación, la idea principal aquí es que algunas veces tiene sentido dividir y luego simplificar y otras veces tiene sentido simplificar y luego dividir. Cualquier orden que elijas, debe llevarte a la misma expresión final.
Ahora pasemos a expresiones radicales que contienen variables. Observa que el proceso de dividirlas es el mismo que el de dividir enteros.
| Ejemplo | ||
| Problema | Simplificar. |
|
|
|
| Usa la regla del cociente elevado a una potencia para reescribir la expresión. |
|
|
| Simplifica |
| Respuesta |
|
|
| Ejemplo | ||
| Problema | Simplificar. |
|
|
|
| Usa la regla del cociente elevado a una potencia para reescribir la expresión. |
|
|
| Simplifica |
|
|
| Identifica cubos perfectos y sácalos del radical. |
|
|
|
|
|
|
| Simplifica. |
| Respuesta |
|
|
Conforma te familiarizas con la división y la simplificación de expresiones radicales, asegúrate de poner atención a las raíces de los radicales que estás dividiendo. Por ejemplo, si bien puedes pensar en 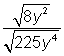 como el equivalente de
como el equivalente de 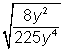 ya que el numerador y el denominador son raíces cuadradas, observa que no puedes expresar
ya que el numerador y el denominador son raíces cuadradas, observa que no puedes expresar 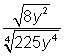 como
como 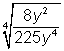 . En este segundo caso, el numerador es una raíz cuadrada y el denominador es una raíz cuarta.
. En este segundo caso, el numerador es una raíz cuadrada y el denominador es una raíz cuarta.
| Divide y simplifica.
A)
B)
C)
D)
|
Sumario
Las reglas del producto elevado a una potencia y del cociente elevado a una potencia pueden usarse para simplificar expresiones radicales siempre y cuando las raíces de los radicales sean las mismas. La regla del producto dice que el producto de dos o más números elevados a una potencia es igual al producto de cada número elevado a la misma potencia. Lo mismo sucede con las raíces: ![]() . Cuando divides expresiones radicales, las reglas que gobiernan a los cocientes son similares:
. Cuando divides expresiones radicales, las reglas que gobiernan a los cocientes son similares: ![]() .
.
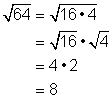
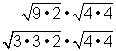
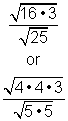
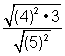
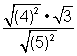
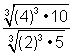
 ,
, 