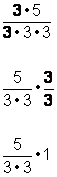Introducción a expresiones racionales

 

Objetivos de aprendizaje

·         Encontrar valores de una variable que hagan indefinida una expresión racional.

·         Simplificar expresiones racionales.

 

 

Las expresiones racionales son fracciones que tienen un polinomio en el numerador, denominador, o ambos. Si bien las expresiones racionales pueden parecer complicadas porque contienen variables, pueden ser simplificadas de la misma forma que se simplifican las fracciones numéricas.

 

 

El primer paso al simplificar una expresión racional es determinar el dominio, el conjunto de todos los valores posibles de las variables. El denominador en una fracción no puede ser cero porque la división entre cero no está definida. La razón es la siguiente: Tenemos  y multiplicas la respuesta 2, por el divisor 3 y obtienes 6. Para poder dividir cualquier número c entre cero  tendrías que encontrar un número que multiplicado por 0 diera c . No existen números que puedan hacer esto, entonces decimos que la “división entre cero no está definida”. Al simplificar expresiones racionales necesitas poner atención a qué valores de las variables en la expresión harían el denominador cero. Estos valores no pueden incluirse en el dominio, por lo que se llaman valores excluidos. Descártalos desde el principio, antes de continuar.

 

(Observa que si bien el denominador no puede ser 0, el numerador sí puede, esta es la razón por la que sólo excluyes valores en el denominador de la expresión racional.)

 

Para las expresiones racionales, el dominio excluye valores para los que el denominador es 0. Dos ejemplos para ilustrar cómo encontrar el dominio de una expresión se muestran a continuación.

 

 

 

 

Encontraste que x no puede ser 4. (Algunas veces verás esta idea presentada como “x ≠ 4.”) ¿Qué sucede si sustituyes este valor en la expresión?

 

 

Cuando x = 4 encuentras que, el numerador se evalúa como 14, pero el denominador se evalúa como 0. Y como la división entre 0 no está definida, esta debe ser un valor excluido.

 

Intentemos con otro un poco más difícil.

 

 

 

 

Encuentra el dominio de la expresión racional . A) todos los números excepto el −4 B) todos los números excepto el 4 C) todos los números excepto el 0 D) todos los números   Mostrar/Ocultar Respuesta A) todos los números excepto el −4 Correcto. Cuando x = −4, el denominador es es 2(−4) + 8 = −8 + 8 = 0. La división entre 0 no está definida, entonces el dominio debe excluir x = −4.   B) todos los números excepto el 4 Incorrecto. Cuando x = 4, el denominador no es igual a 0, entonces no es un valor excluido. Iguala el denominador a 0 y resuelve x. La respuesta correcta es todos los números excepto el −4.   C) todos los números excepto el 0 Incorrecto. Cuando x = 0, el numerador es igual a 0 pero el denominador no, entonces no es un valor excluido. Iguala el denominador a 0 y resuelve x. La respuesta correcta es todos los números excepto el −4.   D) todos los números Incorrecto. Existe un valor de x que hará el denominador 0. Iguala el denominador a 0 y resuelve x. La respuesta correcta es todos los números excepto el −4.

 

 

 

Una vez que has encontrado los valores excluidos, el siguiente paso es simplificar la expresión racional. Para simplificar la expresión racional, sigue el mismo método que usas para simplificar fracciones numéricas: encuentra factores comunes en el numerador y en el denominador. Empecemos simplificando una fracción numérica.

 

 

 

Ahora, habrías podido hacer este problema en la mente, pero vale la pena escribirla, porque así es exactamente como simplificas una expresión racional.

 

Entonces vamos a simplificar una expresión racional, usando la misma técnica que aplicaste para la fracción . Sólo que esta vez, el numerador y el denominador son dos monomios con variables.

 

 

 

 

Observa, los mismos pasos funcionaron. Factoriza el numerador, factoriza el denominador, identifica los factores que son comunes al numerador y al denominador, y escríbelos como un factor de 1 y simplifica.

 

Cuando simplificas expresiones racionales, es un buen hábito siempre considerar el dominio, y encontrar los valores de la variable (o variables) que vuelven la expresión indefinida. (Esto será útil cuando empieces resolviendo variables un poco más adelante.)

 

 

 

Observa que empezaste con la expresión original, para identificar los valores de x que harían 25x igual a 0. ¿Por qué importa esto? Observa  cuando se simplifica ... es la fracción . Como 5 es el denominador, parece que no hay valores para excluirlo del dominio. Cuando buscas el dominio de una expresión, siempre empiezas con la expresión original porque los términos variables podrían ser factorizado como parte del proceso de simplificación.

 

En los ejemplos siguientes, el numerador y el denominador son polinomios con más de un término, pero una vez más, aplican los mismos principios de simplificación. Factoriza el numerador y el denominador para simplificar la expresión racional.

 

 

 

 

 

 

Pasos para simplificar una expresión racional   Para simplificar una expresión racional, sigue los siguientes pasos: ·         Determina el dominio. Los valores excluidos son los valores de la variable que resultarán en una expresión con denominador 0. ·         Factoriza el numerador y el denominador. ·         Encuentra factores comunes para el numerador y el denominador y simplifica.

 

 

Simplifica la siguiente expresión racional.     [Nota: Si bien el dominio y los valores excluidos de una expresión son importantes, no siempre se te pedirá encontrarlos cuando simplificas una expresión racional. En esta expresión, el dominio es todos los números reales excepto y −10.]   A)   B)   C)   D)   Mostrar/Ocultar Respuesta A) Incorrecto. Debes primero factorizar los polinomios en el numerador y en el denominador y luego expresar como 1 factores similares en el numerador y denominador para simplificar. La expresión puede factorizarse como , por lo que la respuesta correcta es .   B) Correcto. La expresión racional puede ser simplificada factorizando el numerador y el denominador como . Ya que , simplifica la expresión a .   C) Incorrecto. Debes primero factorizar los polinomios en el numerador y en el denominador y luego expresar como 1 factores similares en el numerador y denominador para simplificar. La expresión puede factorizarse como , entonces la respuesta correcta es .   D) Incorrecto.  no puede simplificarse a  porque las x’s en el numerador y el denominador no se multiplican, sino que se suman. La respuesta correcta es .

 

 

 

Las expresiones racionales son fracciones que contienen polinomios. Pueden ser simplificadas de la misma manera que las fracciones numéricas. Para simplificar una expresión racional, primero determinas factores comunes en el numerador y en el denominador y luego los eliminas reescribiéndolos como expresiones iguales a 1.

 

Una consideración adicional para las expresiones racionales es determinar qué valores son excluidos del dominio. Como la división entre 0 no está definida, cualquier valor que resulte en un denominador de 0 debe ser excluido. Los valores excluidos deben ser identificados en la ecuación original, no en su forma factorizada.