Sumando y Restando Polinomios
Objetivos de Aprendizaje
· Sumar polinomios.
· Encontrar el opuesto de un polinomio.
· Restar polinomios.
Introducción
Sumar y restar polinomios puede sonar complicado, pero no es tan diferente de la sumas y las restas que haces a diario. La estrategia principal es buscar y combinar términos semejantes.
Puedes sumar dos (o más) polinomios de la misma manera que sumas expresiones algebraicas. Puedes eliminar los paréntesis y combinar los términos semejantes.
| Ejemplo | |||
| Problema | Sumar. (3b + 5) + (2b + 4) | ||
|
| (3b + 2b) + (5 + 4) | Reagrupa usando la propiedad conmutativa de la suma y la propiedad asociativa de la suma. | |
|
| 5b + 9 | Combina términos semejantes. | |
| Respuesta | (3b + 5) + (2b + 4) = 5b + 9 |
| |
| Ejemplo | ||
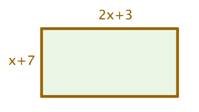
| Problema | Un jardín rectangular tiene un lado con longitud x + 7 y otro con longitud 2x + 3. Encuentra el perímetro del jardín.
| |
|
| (x + 7) + (2x + 3) + (x + 7) + (2x + 3) | El perímetro de un rectángulo es la suma de las longitudes de sus lados. |
|
| (x + 2x + x + 2x) + (7 + 3 + 7 + 3) | Reagrupa por términos semejantes usando las propiedades conmutativa y asociativa. |
|
|
6x + 20 |
Suma términos semejantes. |
|
Respuesta |
El perímetro es 6x + 20. |
|
El procedimiento es el mismo cuando sumas polinomios que contienen coeficientes negativos o resta:
| Ejemplo | ||
| Problema | Sumar. (-5x2 – 10x + 2) + (3x2 + 7x – 4) | |
|
| -5x2 + (-10x) + 2 + 3x2 + 7x + (-4) | Reescribe la resta como la suma de los opuestos. |
|
|
(-5x2 + 3x2) + (-10x + 7x) + (2 – 4) | Reagrupa usando las propiedades conmutativa y asociativa. |
|
|
-2x2 + (-3x) + (-2) |
Combina términos semejantes. |
| Respuesta | (−5x2 – 10x + 2) + (3x2 + 7x – 4) = −2x2 – 3x – 2 | |
Los ejemplos anteriores muestran la suma horizontal de polinomios, al leer de izquierda a derecha en la misma línea. A algunas personas les gusta organizar su trabajo de manera vertical, porque se les hace más fácil asegurarse que están combinando los términos semejantes. El ejemplo siguiente muestra este método “vertical” de sumar polinomios.
| Ejemplo | ||||||||||||||||||||||||
| Problema | Sumar. (3x2 + 2x – 7) + (7x2 – 4x + 8) |
| ||||||||||||||||||||||
|
|
| Escribe un polinomio debajo del otro, asegurándote de alinear los términos semejantes. | ||||||||||||||||||||||
|
|
| Combina los términos semejantes, poniendo atención en los signos. | ||||||||||||||||||||||
| Respuesta | (3x2 + 2x – 7) + (7x2 – 4x + 8) = 10x2 – 2x + 1 | |||||||||||||||||||||||
Algunas veces en un arreglo vertical, puedes alinear cada término debajo de su homólogo, como en el ejemplo anterior. Pero algunas veces no resulta tan ordenado. Cuando no hay un término semejante correspondiente para cada término, habrá espacios vacíos en el arreglo vertical.
| Ejemplo | ||||||||||||||||||||||||||
| Problema | Sumar. (4x3 + 5x2 – 6x + 2) + (−4x2 + 10) |
| ||||||||||||||||||||||||
|
|
| Escribe un polinomio debajo del otro, alineando los términos semejantes.
Deja un espacio en blanco encima o debajo de cada término que no tiene correspondiente. | ||||||||||||||||||||||||
|
|
| Combina los términos semejantes, poniendo atención en los signos. | ||||||||||||||||||||||||
| Respuesta | (4x3 + 5x2 – 6x + 2) + (−4x2 + 10) = 4x3 + x2 – 6x + 12 | |||||||||||||||||||||||||
| Encuentra la suma. (4a2 + 5a + 7) + (8a + 2)
A) 9a2 + 8a + 9
B) 16a2 + 10a
C) 12a2 + 5a + 9
D) 4a2 + 13a + 9
|
Cuando restas polinomios, estás sumando el opuesto, como lo has hecho con los números reales. Entonces ¿cómo encuentras el opuesto de un polinomio? Recuerda que el opuesto de 3 es −3, y el opuesto de −3 es 3. Así como encontramos el opuesto de un número multiplicándolo por −1, podemos encontrar el opuesto de un polinomio multiplicándolo por −1.
| Ejemplo | |||
| Problema | Encontrar el opuesto de 9x2 + 10x + 5. | ||
|
| (−1)(9x2 + 10x + 5) | Encuentra el opuesto multiplicando por −1. | |
|
| (−1)9x2 + (−1)10x + (−1)5
| Distribuye el −1 a cada término del polinomio. | |
|
| −9x2 + (-10x) + (−5)
| Multiplica por −1 cada coeficiente. | |
| Respuesta | El opuesto de 9x2 + 10x + 5 es −9x2 – 10x – 5. | Reescribe la suma de un término negativo como una resta. | |
Ten cuidado cuando ya hay valores negativos o restas en el polinomio.
| Ejemplo | |||
| Problema | Encontrar el opuesto de 3p2 – 5p + 7. | ||
|
| (-1)(3p2 – 5p + 7) | Encuentra el opuesto multiplicando por −1. | |
|
| (-1)[3p2 + (-5)p + 7] | Cambia la resta a la suma del opuesto. | |
|
| (-1)3p2 + (-1)(-5)p + (-1)7
| Distribuye -1 a cada término en el polinomio y multiplica cada coeficiente por -1. | |
|
| -3p2 + 5p + (-7) | Reescribe la suma de un término negativo como una resta. | |
| Respuesta | El opuesto de 3p2 – 5p + 7 es −3p2 + 5p – 7. | ||
Observa que al encontrar el opuesto de un polinomio, cambias el signo de cada término en el polinomio.
| Encuentra el opuesto del polinomio. 8a3 – 3a – 2
A) -8a3 – 3a – 2
B) 8a3 + 3a – 2
C) 8a3 + 3a + 2
D) -8a3 + 3a + 2
|
De la misma manera que restar números reales es lo mismo que sumar el opuesto, puedes restar polinomios sumando el opuesto del segundo polinomio. Veamos un ejemplo:
| Ejemplo | |||
| Problema | Restar. (15x2 + 12x + 20) – (9x2 + 10x + 5) | ||
|
| (15x2 + 12x + 20) + (-9x2 – 10x – 5) | Cambia la resta por la suma con el opuesto. ¡Ten cuidado de cambiar el signo de cada término! | |
|
| (15x2 + -9x2) + (12x – 10x) + (20 – 5) | Reagrupa para organizar los términos. | |
|
| 6x2 + 2x + 15 | Combina los términos semejantes. | |
| Respuesta | (15x2 + 12x + 20) – (9x2 + 10x + 5) = 6x2 + 2x + 15 | ||
Cuando los polinomios incluyen muchos términos, puede ser fácil perderle la pista los signos. Ten cuidado de transferirlos correctamente, especialmente cuando restas un término negativo.
| Ejemplo | ||
| Problema | Restar. (14x3 + 3x2 – 5x + 14) – (7x3 + 5x2 – 8x + 10) | |
|
| (14x3 + 3x2 – 5x + 14) + (-7x3 – 5x2 + 8x – 10) | Reescribe como la suma con el opuesto. |
|
| 14x3 + 3x2 + (-5)x + 14 + (-7)x3 + (-5)x2 + 8x +(-10) | Podrías reescribir todas las restas como la suma de sus opuestos. |
|
| 14x3 + (-7)x3 + 3x2 + (-5)x2 + (-5)x + 8x + 14 + (-10) | Reagrupa para juntar los términos semejantes. |
|
| 7x3 + (-2)x2 + 3x + 4 | Combina los términos semejantes. |
| Respuesta | (14x3 + 3x2 – 5x + 14) – (7x3 + 5x2 – 8x + 10) = 7x3 – 2x2 + 3x + 4 | |
Problemas complejos, como el de arriba, pueden resolverse más fácilmente usando el método vertical (mostrado abajo). Sin embargo la manera en la que combinas los polinomios es decisión tuya — lo importante es identificar los términos semejantes, y poder organizarlos sin equivocarte.
| Ejemplo | |||||||||||||||||||||||||||||
| Problema | Restar. (14x3 + 3x2 – 5x + 14) – (7x3 + 5x2 – 8x + 10) | ||||||||||||||||||||||||||||
|
|
| Reorganiza usando el método vertical. | |||||||||||||||||||||||||||
|
|
| Cambia la resta por la suma de los opuestos, y combina los términos semejantes. | |||||||||||||||||||||||||||
| Respuesta | (14x3 + 3x2 – 5x + 14) – (7x3 + 5x2 – 8x + 10) = 7x3 – 2x2 + 3x + 4 | ||||||||||||||||||||||||||||
De la misma forma que con las operaciones con enteros, la experiencia y la práctica hacen más fácil sumar y restar polinomios.
| Restar. (4a3 – 5a + 7) – (8a3 – 3a – 2)
A) -4a3 – 8a + 5
B) --4a3 + 3a + 9
C) -4a3 – 2a + 9
D) -4a3 + 2a + 5
|
Sumario
Cuando sumes o restes polinomios, usa las propiedades conmutativa y asociativa para reagrupar términos los en un polinomio en grupos de términos semejantes. Cambia la resta, incluyendo la resta del segundo polinomio, a la suma del opuesto. Cuando encuentres el opuesto de un polinomio, asegúrate de cambiar el signo de cada término. Luego puedes combinar los términos semejantes.