Introduction to Single Variable Polynomials

 

Learning Objective(s)

·         Identify the terms, the coefficients and the exponents of a polynomial.

·         Evaluate a polynomial for given values of the variable.

·         Simplify polynomials by collecting like terms.

 

 

 

Algebraic expressions are created by combining numbers and variables using arithmetic operations: addition, subtraction, multiplication, division, and exponentiation. Using all but division, you can create an expression called a polynomial by adding or subtracting terms. Polynomials are very useful in applications from science and engineering to business. Monomials (and polynomials in general) may have more than one variable, but in this unit, you will only work with single variable polynomials.

 

 

 

The basic building block of a polynomial is a monomial. A monomial is one term and can be a number, a variable, or the product of a number and variables with an exponent. The number part of the term is called the coefficient.

 

 

 

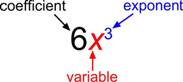
The coefficient can be any real number, including 0. The exponent of the variable must be a whole number—0, 1, 2, 3, and so on. A monomial cannot have a variable in the denominator or a negative exponent.

 

The value of the exponent is the degree of the monomial. Remember that a variable that appears to have no exponent really has an exponent of 1. And a monomial with no variable has a degree of 0. (Since x⁰ has the value of 1 if x ≠ 0, a number such as 3 could also be written 3x⁰, if x ≠ 0. as 3x⁰ = 3 • 1 = 3.)

 

 

 

 

 

 

Identify the coefficient, variable, and exponent of 3y.   A) The variable is y, the exponent is 3, and the coefficient is 1. B) The variable is y, the exponent is 0, and the coefficient is 3. C) The variable is y, the exponent is 1, and the coefficient is 3. D) The variable is y, the exponent is 3, and the monomial has no coefficient.   Show/Hide Answer A) The variable is y, the exponent is 3, and the coefficient is 1. Incorrect. The exponent is the power of the variable and the coefficient is the number before the variable. The coefficient in this case is 3, and the exponent is 1 because 3y = 3y1.   B) The variable is y, the exponent is 0, and the coefficient is 3. Incorrect. The coefficient is 3, but the exponent is 1 because 3y = 3y1. An exponent of 0 would be 3y0, and since y0 = 1 when y ≠ 0, this would be equal to 3 (when y ≠ 0).   C) The variable is y, the exponent is 1, and the coefficient is 3. Correct. The coefficient is 3, the variable is y, and the exponent is 1 because 3y = 3y1.   D) The variable is y, the exponent is 3, and the monomial has no coefficient. Incorrect. The exponent is the power of the variable and the coefficient is the number before the variable. The coefficient in this case is 3, and the exponent is 1 because 3y = 3y1.

 

 

 

A polynomial is a monomial or the sum or difference of two or more polynomials. Each monomial is called a term of the polynomial.

 

Some polynomials have specific names indicated by their prefix.

 

monomial – is a polynomial with exactly one term (“mono” – means one)

binomial – is a polynomial with exactly two terms (“bi” – means two)

trinomial – is a polynomial with exactly three terms (“tri” – means three)

 

The word “polynomial” has the prefix, “poly,” which means many. However, the word polynomial can be used for all numbers of terms, including only one term.

 

Because the exponent of the variable must be a whole number, monomials and polynomials cannot have a variable in the denominator.

 

Polynomials can be classified by the degree of the polynomial. The degree of a polynomial is the degree of its highest degree term. So the degree of 2x³ + 3x² + 8x + 5 is 3.

 

A polynomial is said to be written in standard form when the terms are arranged from the highest degree to the lowest degree. When it is written in standard form it is easy to determine the degree of the polynomial.

 

The table below illustrates some examples of monomials, binomials, trinomials, and other polynomials. They are all written in standard form.

 

 

When the coefficient of a polynomial term is 0, you usually do not write the term at all (because 0 times anything is 0, and adding 0 doesn’t change the value). The last binomial above could be written as a trinomial, 14y³ + 0y² + 3y.

 

A term without a variable is called a constant term, and the degree of that term is 0. For example 13 is the constant term in 3y + 13. You would usually say that 14y³ + 3y has no constant term or that the constant term is 0.

 

 

Which of the following expressions are polynomials?   2x4 − 3x3   14     A) Only 2x4 − 3x3 and  are polynomials. B) Only 2x4 − 3x3 and 14 are polynomials. C) Only 2x4 − 3x3 is a polynomial. D) None of the expressions is a polynomial.   Show/Hide Answer A) Only 2x4 − 3x3 and  are polynomials. Incorrect.  is not a polynomial because it has a variable in the denominator. The correct answer is 2x4 – 3x3 and 14.   B) Only 2x4 − 3x3 and 14 are polynomials. Correct.  is not a polynomial because it has a variable in the denominator.   C) Only 2x4 − 3x3 is a polynomial. Incorrect. 14 is also a monomial, a type of polynomial. The correct answer is 2x4 – 3x3 and 14.   D) None of the expressions is a polynomial. Incorrect. x4 – 3y3 and 14 are polynomials.  is not a polynomial because it has a variable in the denominator.

 

 

 

You can evaluate polynomials just as you have been evaluating expressions all along. To evaluate an expression for a value of the variable, you substitute the value for the variable every time it appears. Then use the order of operations to find the resulting value for the expression.

 

 

 

 

 

 

Evaluate 3x3 − 2x2 for x = -2.   A) -24 – 2x2 B) -32 C) -16 D) 16     Show/Hide Answer A) -24 – 2x2 Incorrect. x = -2 for all appearances of x in the expression. You must substitute -2 into both instances: 3(-2)3 – 2(-2)2. The correct answer is -32.   B) -32 Correct. Since x = -2, 3x3 − 2x2 = 3(-2)3 – 2(-2)2 = 3(-8) – 2(4) = -24 – 8 = -32.   C) -16 Incorrect. You may have forgotten that (-2)2 is positive, or made another mistake in your calculations. Since x = -2, 3x3 − 2x2 = 3(-2)3 – 2(-2)2 = 3(-8) – 2(4) = -24 – 8 = -32.   D) 16 Incorrect. You may have forgotten that (-2)3 is negative (the product of two negative values is positive, so multiplying by a third negative gives a negative product). Since x = -2, 3x3 − 2x2 = 3(-2)3 – 2(-2)2 = 3(-8) – 2(4) = -24 – 8 = -32.

 

 

 

A polynomial may need to be simplified. One way to simplify a polynomial is to combine the like terms if there are any. Two or more terms in a polynomial are like terms if they have the same variable (or variables) with the same exponent. For example, 3x² and -5x² are like terms: They both have x as the variable, and the exponent is 2 for each. However, 3x² and 3x are not like terms, because their exponents are different.

 

Here are some examples of terms that are like and some that are unlike.

 

 

 

 

 

 

Which of these are like terms?   −3a   3a2   8b   −3b3   8a   14b2   9a   A) Only −3a, 8a, and 9a are like terms. B) Only 8a and 9a are like terms. C) 8b, −3b3, and 14b2 are like terms, and −3a, 3a2, 8a, and 9a are like terms. D) 3a2 and 14b2  are like terms, and −3a, 8b, 8a, and 9a are like terms.   Show/Hide Answer A) Only −3a, 8a, and 9a are like terms. Correct. These terms have the same variable, a, with an exponent of 1.   B) Only 8a and 9a are like terms. Incorrect. -3a also is a like term with 8a and 9a, because it has the same variable with the same exponent.   C) 8b, −3b3, and 14b2 are like terms, and −3a, 3a2, 8a, and 9a are like terms. Incorrect. Each group has the same variable, but their exponents are different. The only terms with the same variable and exponent are −3a, 8a, and 9a.   D) 3a2 and 14b2  are like terms, and −3a, 8b, 8a, and 9a are like terms. Incorrect. Each group has the same exponent, but their variables are different. The only terms with the same variable and exponent are −3a, 8a, and 9a.

 

 

You can use the distributive property to simplify the sum of like terms. Recall that the distributive property of addition states that the product of a number and a sum (or difference) is equal to the sum (or difference) of the products.

 

                        2(3 + 6) = 2(3) + 2(6)

 

Both expressions equal 18. So you can write the expression in whichever form is the most useful.

 

Let’s see how we can use this property to combine like terms.

 

 

 

 

You may have noticed that combining like terms involves combining the coefficients to find the new coefficient of the like term. You can use this as a shortcut.

 

 

 

 

When you have a polynomial with more terms, you have to be careful that you combine only like terms. If two terms are not like terms, you can’t combine them.

 

 

 

 

Simplify by combining like terms.   -3a + 3a2 + 8a + 9a – 3   A) 3a2 + 17a – 3 B) 3a2 + 14a – 3 C) 17a – 3 D) 17a – 3a – 3   Show/Hide Answer A) 3a2 + 17a – 3 Incorrect. There are three terms with a (remember that a1 is written as a): -3a, 8a, and 9a. Combining them gives -3a + 8a + 9a = (-3 + 8 + 9)a = 14a, so the simplified polynomial is 3a2 + 14a – 3.   B) 3a2 + 14a – 3 Correct. There are three terms with a (remember that a1 is written as a): -3a, 8a, and 9a. Combining them gives -3a + 8a + 9a = (-3 + 8 + 9)a = 14a, so the simplified polynomial is 3a2 + 14a – 3.   C) 17a – 3 Incorrect. You may have incorrectly combined the first two terms, -3a + 3a2. These are not like terms, so you can’t combine them. There are three terms with a (remember that a1 is written as a): -3a, 8a, and 9a. Combining them gives -3a + 8a + 9a = (-3 + 8 + 9)a = 14a, so the simplified polynomial is 3a2 + 14a – 3.   D) 17a – 3a – 3 Incorrect. There are three terms with a (remember that a1 is written as a): -3a, 8a, and 9a. Combining them gives -3a + 8a + 9a = (-3 + 8 + 9)a = 14a, so the simplified polynomial is 3a2 + 14a – 3.

 

 

 

Polynomials are algebraic expressions that contain any number of terms combined by using addition or subtraction. A term is a number, a variable, or a product of a number and one or more variables with exponents. Like terms (same variable or variables raised to the same power) can be combined to simplify a polynomial. The polynomials can be evaluated by substituting a given value of the variable into each instance of the variable, then using order of operations to complete the calculations.