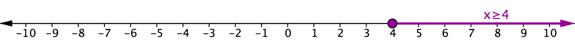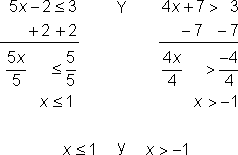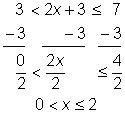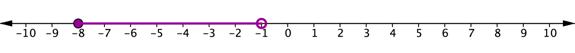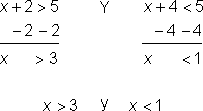Desigualdades Compuestas
Objetivos de Aprendizaje
· Resolver desigualdades compuestas de tipo o y expresar la solución gráficamente.
· Resolver desigualdades compuestas de tipo y y expresar la solución gráficamente.
· Resolver desigualdades compuestas de tipo a < x < b.
· Identificar casos sin solución.
Introducción
Muchas veces, las soluciones se encuentran entre dos desigualdades, en lugar de continuar infinitamente en una dirección. Por ejemplo la presión sanguínea sistólica que está entre 120 y 139 mm Hg se llama límite superior de alta presión. Esto se puede expresar usando una desigualdad compuesta, b < 139 y b > 120. Otras desigualdades compuestas se unen con la palabra “o”.
Cuando dos desigualdades se unen con la palabra y, la solución de la desigualdad compuesta ocurre cuando ambas desigualdades son válidas al mismo tiempo. Es la superposición, o intersección, de la soluciones para cada desigualdad. Cuando las dos desigualdades están unidad por la palabra o, la solución de la desigualdad compuesta ocurre cuando cualquiera de las desigualdades es válida. La solución es la combinación, o unión, de dos soluciones individuales.
Echemos un vistazo a la desigualdad compuesta que usa o para combinar dos desigualdades. Por ejemplo, x > 6 o x < 2. La solución de la desigualdad compuesta es todos los valores de x en los que x es ambos mayor que 6 o menor que 2. Puedes ver esto gráficamente poniendo juntas las gráficas de cada desigualdad en la misma recta numérica.

La gráfica tiene un círculo abierto en 6 y una flecha azul hacia la derecha y otro círculo abierto en 2 y una flecha roja a la izquierda. De hecho, las únicas partes que no son solución a esta desigualdad compuesta son los puntos 2 y 6 y todos los puntos entre estos dos valores de la recta numérica. Todo lo demás en la gráfica es una solución de la desigualdad compuesta.
Veamos otro ejemplo de una desigualdad compuesta de tipo o, x > 3 o x ≤ 4. La gráfica de x > 3 tiene un círculo abierto y una flecha azul dibujada hacia la derecha para contener todos los números mayores que 3.
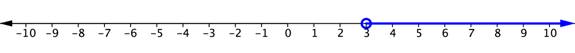
La gráfica de x ≤ 4 tiene un círculo cerrado y una flecha roja dibujada hacia la izquierda para contener todos los números menores que.

¿Qué notas sobre la gráfica que combina estas dos desigualdades?

Como la desigualdad compuesta es un enunciado o, incluye todos los números en cada una de las soluciones, las cuales en este caso son todos los números de la recta numérica. (La región de la línea mayor que 3 y menor o igual a 4 se muestra en morado porque pertenece a ambas gráficas originales.) ¡La solución de la desigualdad compuesta x > 3 o x ≤ 4 es el conjunto de números reales!
Podrías necesitar resolver una o más de las desigualdades antes de determinar la solución de la desigualdad compuesta, como se muestra a continuación.
| Ejemplo | |||||
| Problema | Resolver x. 3x – 1 < 8 o x – 5 > 0 |
| |||
|
| Resolver cada desigualdad despejando la variable.
Escribir ambas soluciones como un compuesto usando o. | ||||
| Respuesta |
|
|
| ||
La solución a esta desigualdad compuesta puede mostrarse gráficamente.

Recuerda aplicar las propiedades de la desigualdad cuando estés resolviendo desigualdades compuestas. El siguiente ejemplo implica dividir entre un negativo para despejar la variable.
| Ejemplo | ||||
| Problema | Resolver y. 2y + 7 < 13 o −3y – 2 |
| ||
|
| Resolver separadamente cada desigualdad.
El signo de desigualdad es revertido por la división de un número negativo.
Como y podría ser menor que 3 o mayor o igual a −4, y podría ser cualquier número. | |||
| Respuesta |
| La solución son todos los números reales. |
| |
Esta recta numérica muestra el conjunto solución de y < 3 o y ≥ 4.

| Ejemplo | ||||
| Problema | Resolver z. 5z – 3 > −18 o −2z – 1 > 15 |
| ||
|
| Resolver separadamente cada desigualdad.
Combina las soluciones. | |||
| Respuesta |
|
|
| |
Esta recta numérica muestra el conjunto solución de z > −3 o z < −8.

| Resolver h. h + 3 > 12 o 3 – 2h > 9
A) h < 3 o h > −3 B) h > 9 o h > −3 C) h > −9 o h < 3 D) h > 9 o h < −3
|
La solución de desigualdades compuestas que consisten en dos desigualdades unidad por la palabra y es la intersección de las soluciones de cada desigualdad. En otras palabras, ambos enunciados deben ser válidos al mismo tiempo. La solución de una desigualdad compuesta de tipo y son todas las soluciones que tengan en común las dos desigualdades. Gráficamente, puedes pensar en esto como si fueran dos gráficas que se sobreponen.
Piensa en el ejemplo de la desigualdad compuesta: x < 5 y x ≥ −1. La gráfica de cada desigualdad individual se muestra en color.

Como la palabra y une las dos desigualdades, la solución es la superposición de las dos soluciones. Esto es donde ambos enunciados son válidos al mismo tiempo.
La solución de esta desigualdad compuesta se muestra abajo.

Observa que en este caso, puedes reescribir x ≥ −1 y x < 5 como −1 ≤ x < 5 ya que la solución está entre −1 y 5, incluyendo −1. Lees −1 ≤ x < 5 como “x es mayor que o igual a −1 y menor que 5.” Puedes reescribir un enunciado y de esta manera sólo si la respuesta está entre dos números.
Veamos otros dos ejemplos.
| Ejemplo | ||||
| Problema | Resolver x.
|
| ||
|
| Resolver cada desigualdad para x.
Determinar la intersección de las soluciones. | |||
| La recta numérica de abajo muestra las gráficas de las dos desigualdades del problema. La solución a la desigualdad compuesta es x ≥ 4, porque ahí es donde las dos desigualdades se superponen.
| ||||
| Respuesta |
|
|
| |
| Ejemplo | ||||
| Problema | Resolver x.
|
| ||
|
| Resuelve separadamente cada desigualdad.
Encuentra la superposición entre las soluciones. | |||
| Las dos desigualdades pueden representarse gráficamente como:
Y la solución puede representarse como:
| ||||
| Respuesta |
|
|
| |
En lugar de dividir una desigualdad compuesta en la forma de a < x < b en dos desigualdades x < b y x > a, puedes resolver la desigualdad más rápido aplicando las propiedades de la desigualdad a los tres segmentos de la desigualdad compuesta. Dos ejemplos se muestran a continuación.
| Ejemplo | |||||
| Problema | Resolver x.
|
| |||
|
| Despeja la variable restando 3 de todas las partes de la desigualdad, y luego divide entre 2 cada parte.
| ||||
| Respuesta |
|
| |||
| Ejemplo | |||||
| Problema | Resolver x.
|
| |||
|
| Despeja la variable restando 7 de todas las partes de la desigualdad, y luego divide entre 2 cada parte. | ||||
| Respuesta |
|
| |||
Para resolver desigualdades de tipo a < x < b, usa las propiedades de la adición la multiplicación de la desigualdad para resolver la desigualdad para x. Cualquier operación que hagas en la porción media de la desigualdad, debes también realizarla en las secciones exteriores. Pon especial atención a la división o multiplicación por un negativo.
| ¿Cuál de las siguientes desigualdades compuestas representa la gráfica en la recta numérica de abajo?
A) −8 ≥ x > −1 B) −8 ≤ x < −1 C) −8 ≤ x > −1 D) −8 ≥ x < −1
|
La solución a una desigualdad compuesta con y siempre es la superposición entre la solución de cada desigualdad. Existen tres resultados posibles para las desigualdades compuestas unidas por la palabra y:
1. La solución podría ser todos los valores entre los dos puntos finales.


2. La solución podría empezar en un punto de la recta numérica y extenderse en una dirección.

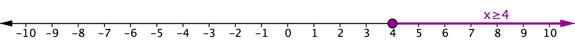
3. En los casos donde no hay superposición entre las dos desigualdades, no hay solución a la desigualdad compuesta.
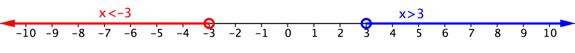
Un ejemplo se muestra a continuación.
| Ejemplo | ||||
| Problema | Resolver x. x + 2 > 5 y x + 4 < 5 |
| ||
|
| Resolver separadamente cada desigualdad.
Encontrar la superposición entre las soluciones. | |||
|
| ||||
| Respuesta No hay superposición entre |
| |||
Sumario
Una desigualdad compuesta es un enunciado de dos desigualdades unidas ya sea por la palabra o o por la palabra y. A veces, una desigualdad compuesta de tipo y se muestra simbólicamente, como a < x < b, y no necesita llevar la palabra y. Como las desigualdades compuestas representan ya sea una unión o una intersección de las desigualdades individuales, graficarlas en una recta numérica puede ser una manera útil para ver o comprobar la solución. Las desigualdades compuestas pueden manipularse y resolverse de la misma forma que se resuelven las desigualdades, poniendo atención a las propiedades de la desigualdad y sus reglas de solución.
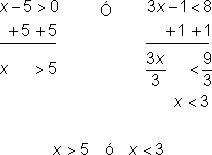
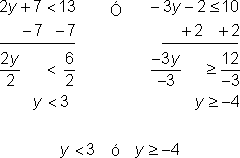
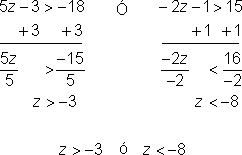
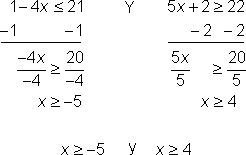
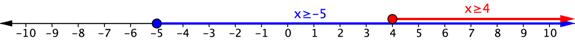 Y la solución puede representarse como:
Y la solución puede representarse como: