Uso y abuso de las representaciones gráficas
Objetivos de aprendizaje
· Identificar qué tipo de grafica representa mejor los datos en determinada situación.
· Explicar cómo las gráficas pueden llevar a la interpretación errónea de los datos.
Introducción
Además de las gráficas de barras, histogramas, y gráficas circulares (de pastel), existen otras gráficas que se usan en la estadística para representar datos y analizar lo que contienen. Pero debes ser cuidadoso cuando creas o lees gráficas. Si no fueron construidas cuidadosamente pueden ser engañosas, y a veces las personas las hacen así a propósito.
Elegir qué tipo de gráfica usar para representar datos específicos es cuestión de prueba y error. Y, algunas veces, existe más de un tipo de gráfica apropiada que puedes usar. Lo que elijas depende de la manera en la que quieres representar tus datos, así como tus preferencias personales. Los programas modernos de hojas de cálculo como Excel son muy flexibles para crear diferentes tipos de gráficas; con un par de clics puedes ver los datos representados como una gráfica de barras, una gráfica lineal, o una gráfica circular. De ahí, puedes escoger cuál es la que mejor representa la idea que quieres mostrar.
Como hay muchas formas de representar un conjunto de datos con una gráfica, veamos algunos ejemplos y pensemos en las distintas posibilidades que tenemos disponibles.
| Ejemplo | ||
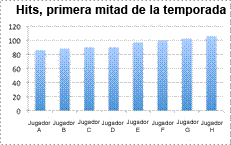
| Problema | Un publicista de beisbol quiere crear una gráfica mostrando el número total de hits de los jugadores con el mayor número de hits en la primera mitad de la temporada. Estos jugadores tienen el siguiente número de hits: 86, 88, 90, 90, 97, 99, 102 y 106.
¿Qué tipo de gráfica debe usar el publicista para representar los datos? | |
|
|
| El conjunto de datos contiene información sobre el total de hits de 8 jugadores. Ya sea una gráfica de barras o un pictograma pueden ayudar a mostrar el número total de hits por cada jugador y compararlos con otros jugadores. |
|
|
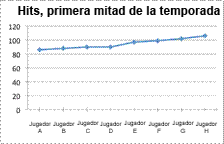
| Una gráfica lineal no sería apropiada, porque los datos no son continuos — no hay datos “entre” los totales de cada jugador. |
|
|
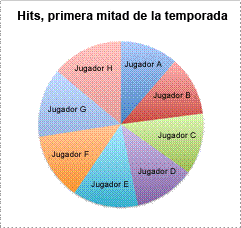
| Una gráfica circular tampoco tiene sentido, a menos que el publicista quiera mostrar el porcentaje de hits que tiene cada jugador del total número de hits. Pero esos datos no serían muy útiles si el publicista sólo quiere mostrar el número total de hits.
|
| Respuesta | Una gráfica de barras o un pictograma sería lo mejor. (Un pictograma podría ser más útil, pues la cantidad de datos es pequeña.) | |
El publicista podría usar una gráfica de tallo-hoja para mostrar la distribución de los datos numéricos, pero este tipo de gráfica no es tan efectiva para mostrar la relación entre cada jugador y el número de hits que tiene. Un diagrama de caja y bigote, que muestra los datos medios de un conjunto, tampoco sería útil aquí — El publicista está interesado en los hits totales, no en el promedio de hits o la extensión de los datos.
| Ejemplo | ||
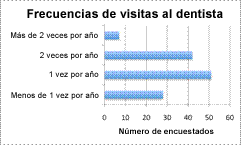
| Problema | Un estadístico está recolectando datos de la frecuencia con los adultos van al dentista. Entrevista a 128 personas y obtiene la siguiente información.
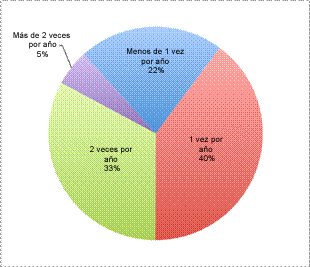
Menos de una vez al año: 28 encuestados 1 vez al año: 51 encuestados 2 veces al año: 42 encuestados Más de dos veces al año: 7 encuestados
En una presentación de dentistas, él quiere destacar la población que visita al dentista menos de una vez al año. ¿Qué tipo de gráfica le ayudaría para representar los datos? | |
|
|
| Para mostrar los resultados, el estadístico podría usar dos tipos de gráficas. Una gráfica de barras sería buena idea porque los datos son categóricos — se quiere agrupar los resultados en 4 categorías. |
|
|
| Una gráfica circular podría ser mejor. Nos interesa el porcentaje de personas que respondieron el cuestionario. Una gráfica circular permite una fácil comparación entre las categorías estudiadas. |
| Respuesta | Lo mejor es usar una gráfica circular, pero una gráfica de barras también funcionaría. | |
Al igual que el primer ejemplo, las gráficas de tallo-hoja y los diagramas de caja y bigote no son útiles aquí. El estadístico no está interesado en el promedio de las veces que va una persona al dentista. Una gráfica lineal tampoco sería apropiada, pues los datos no son continuos.
| Ejemplo | ||
| Problema | El director de un parque de diversiones quiere entender mejor la distribución de tiempos de espera que las personas experimentan cuando están formadas en un juego. Un día les pregunta a 15 personas al azar sobre el tiempo que deben esperar (en minutos).
12, 3, 2, 10, 12, 0, 2, 0, 8, 5, 4, 0, 7, 4, 6
¿Qué tipo de gráfica provee la mejor representación visual de este conjunto de datos: una gráfica circular, un diagrama de caja y bigote, o una gráfica de barras? | |
|
|
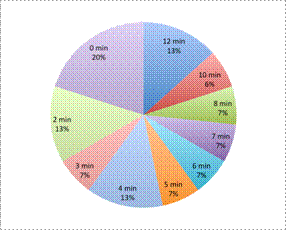
| La idea principal es que el administrador quiere entender la distribución de tiempos de espera. Una gráfica circular no muestra esa distribución. El administrador podría crear una gráfica circular (como la de la izquierda) que muestre el porcentaje de personas que esperan por diferentes espacios de tiempo, pero esto no ayuda a entender la distribución de los datos. |
|
|
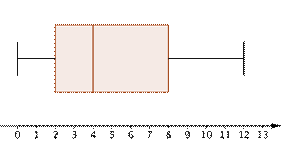
| Crear un diagrama de caja y bigote sería más útil. Este tipo de gráfica mostraría efectivamente la distribución, como se muestra a la izquierda. La mitad de las personas esperan entre 2 y 8 minutos para un juego. |
|
|
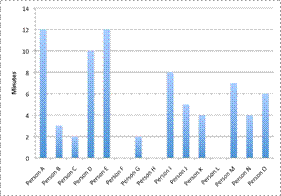
| Una gráfica de barras puede mostrar la longitud de tiempo que cada persona espera, pero no muestra mucho sobre la distribución de esos tiempos. |
| Respuesta | Lo mejor es usar un diagrama de caja y bigote. | En última instancia, el diagrama de caja y bigote da más información acerca de la distribución, por lo que es el más útil. |
| Un oceanógrafo quiere hacer una gráfica que muestre la altura (en cm) de un tipo de coral en un periodo de 2 años. ¿Qué tipo de gráfica sería la más apropiada?
A) Gráfica circular B) Diagrama de caja y bigote C) Gráfica lineal D) Gráfica de tallo-hoja
|
Como lo has visto, las gráficas proveen una manera visual de representar conjuntos de datos. Sin embargo, las imágenes pueden ser engañosas, por lo que también debes saber cómo identificar gráficas que parecen mostrar algo distinto de lo que dicen los datos. Esto puede ser causa del descuido o puede hacerse a propósito. Abajo hay algunas preguntas generales que puedes tener en cuenta al momento de leer una gráfica.
| Preguntas a considerar cuando leemos gráficas
· ¿Está la gráfica bien etiquetada? · ¿Cuál es la escala? · ¿Muestra la gráfica una visión completa de los datos, o sólo una fracción de la idea?
|
Observa la gráfica siguiente. El título dice “Salario Promedio de los Profesores Adjuntos en los Cuatro Colegios,” y aparecen cuatro barras en la gráfica. Puedes saber qué colegios están siendo comparados, pero no te da información sobre la escala usada. La gráfica hace parecer que el salario promedio de los Profesores Adjuntos del Colegio Central es mucho mayor que el de los Profesores Adjuntos del Colegio del Este, pero sin una escala, no podemos estar seguros. (Sabemos que el salario es mayor — pero no sabemos por cuánto.) Para hacer esta gráfica menos engañosa, debe incluirse un eje-y con la información de salario.
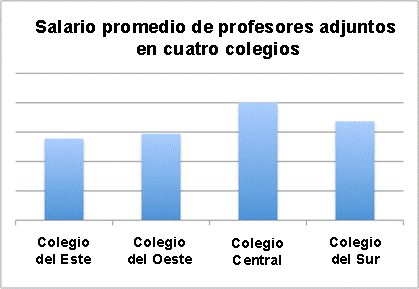
Incluso cuando ambos ejes son presentados y etiquetados correctamente, las representaciones gráficas pueden ser engañosas. Esto se muestra en el conjunto de gráficas de asistencia mostradas a continuación.
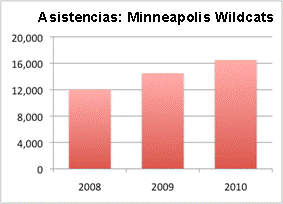
En la gráfica de la izquierda, la escala inicia en 0 y va hasta 20,000. La gráfica por sí misma muestra que la asistencia a los juegos de los Minneapolis Wildcats ha aumentado cada año desde 2008, alcanzando su tope en 2010 con poco más de 16,000 asistentes.
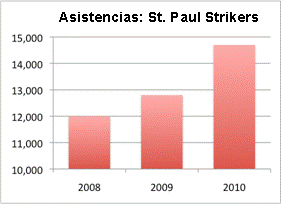
Ahora veamos la gráfica de la derecha. Aparentemente muestra que la asistencia a los juegos de los St. Paul Strikers ha incrementado aún más — la barra de 2010 es el doble de alto que la barra de 2008. Al observar estas dos gráficas, podríamos concluir que los Strikers ha sido el equipo más popular recientemente, porque la altura de las barras parece indicar que la asistencia ha crecido más rápido que la de los Wildcats.
Pero observa con detenimiento. La escala de la gráfica de los Strikers es muy distinta — ¡empieza a los 10,000! Esto pinta una idea engañosa de los datos cuando los comparamos con la gráfica de los Wildcats, que empieza en 0. Y si observamos más detenidamente a los datos (la asistencia, no sólo la altura de las barras), puedes ver que la asistencia en realidad es mayor para los juegos de los Wildcats. En 2010, por ejemplo, la asistencia fue de poco más de 16,000, mientras que la asistencia de los Strikers no pasó de los 15,000.
Esto señala un punto importante. Cuando hacemos gráficas para comparar conjuntos de datos, las escalas deben ser consistentes — de otra manera es muy difícil comparar los datos. Como puedes ver de las dos gráficas anteriores, cambiar la escala de la gráfica cambia dramáticamente la manera en la que se ven y crean una impresión.
Una representación más honesta de los datos de asistencia puede hacerse con una gráfica de barras doble, donde aparece la asistencia de ambos equipos una al lado de la otra en la misma escala. Observa los resultados abajo. Ahora es claro que la asistencia de los Wildcats ha sido mayor que la de los Strikers.
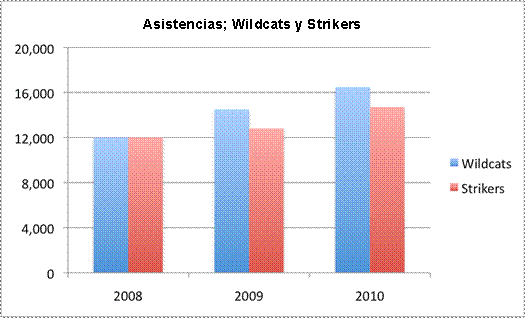
La siguiente gráfica circular es otro ejemplo de una representación engañosa. Los porcentajes reales de las personas que respondieron a cada pregunta no están disponibles, y el observador tiene que interpretar los datos basado en el tamaño de las secciones. A primera vista, la gráfica parece mostrar que muchos votantes favorecen al Candidato A, porque la sección con “Si” es muy grande.
Parte de la razón por la que esta sección parece más grande es porque la gráfica fue creada para que se viera más grande. La gráfica circular está representada de manera tridimensional, y los datos que están más hacia adelante — la rebanada de “Si” — aparecen de manera más prominente. ¡El creador de esta gráfica quiere que pienses que el Candidato A es muy popular!

Una inspección más detenida, muestra que los datos realmente no representan esto. Si combinamos las secciones “Si” y “Probablemente Si” resulta casi lo mismo que combinar las secciones “No” y “Probablemente No”, lo que significa que el candidato no es tan popular como lo muestra la representación. De hecho, alguien que no quiera que este candidato aparezca popular, puede representar los datos usando la siguiente gráfica. Observa que han cambiado las posiciones de las secciones “No” y “Probablemente No”, así como la consistencia de los colores.
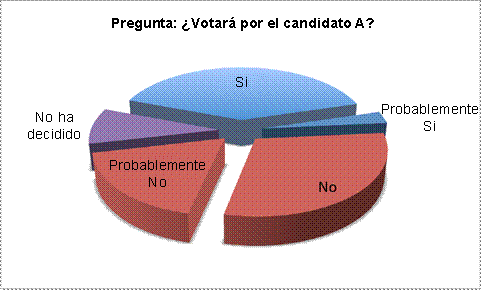
¿Notas cómo la perspectiva y el color hacen la diferencia al ver y analizar los datos?
A continuación se muestra una manera más honesta de representar los datos. En la gráfica, se muestra la misma gráfica circular de arriba, y los porcentajes están incluidos.
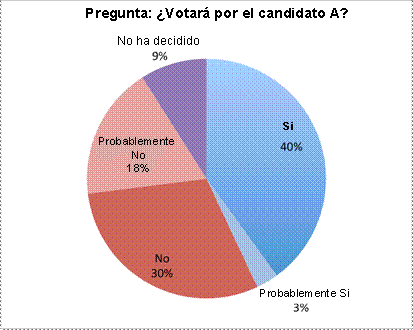
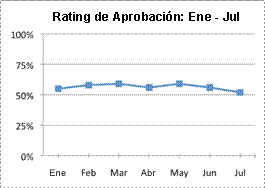
| Los resultados de una encuesta midiendo el índice de aprobación de un político se muestran en la siguiente tabla.
¿Cuál de las siguientes gráficas es la más engañosa?
A)
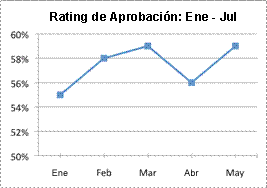
B)
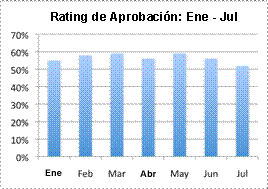
C)
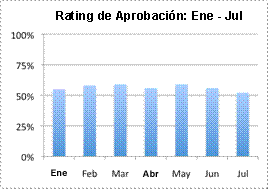
D)
|
Sumario
Las gráficas tienen un gran impacto en cómo entendemos un conjunto de datos. Si usas el tipo apropiado de gráfica puedes comunicar tus datos efectivamente; sin embargo, si usas el tipo incorrecto de gráfica, tus lectores no entenderán la historia que quieres transmitir. Cuando leas gráficas en los periódicos y en el internet, asegúrate de ver los ejes, la escala, y la presentación misma de los datos. Esto te puede ayudar a identificar si la gráfica muestra justa o injustamente el conjunto de datos.