Otros tipos de gráficas
Objetivos de aprendizaje
· Leer e interpretar datos a partir de gráficas circulares (pastel).
· Leer e interpretar datos a partir de gráficas lineales.
· Leer e interpretar datos a partir de gráficas de tallo-hoja.
Introducción
Gráficas diferentes cuentan historias diferentes. Si bien una gráfica de barras puede ser apropiada para comparar algunos tipos de datos, existen otros tipos de gráficas que pueden representar datos de una manera distinta. Puedes verlas en las noticias o en los deportes, por lo que es útil saber cómo leerlas e interpretarlas.
Algunas veces verás datos categóricos presentados en una gráfica circular, o pastel. En este tipo de gráficas, piezas individuales de datos son representadas como secciones de un círculo (o “rebanadas de pastel”). Las gráficas circulares normalmente se usan para mostrar cómo un conjunto de datos se divide en componentes individuales.
Aquí hay un ejemplo. Al inicio del semestre, una maestra describe la forma de calificar a sus estudiantes. Dice, “La mitad de la calificación se va a basar en el examen final y 20% va a determinarse con exámenes parciales. El proyecto valdrá 20% y a la participación en clase le correspondería el 10%.” Para decirle esto a su clase, también pudo haber creado una gráfica circular.

Esta gráfica es útil porque relaciona cada parte — el examen final, los exámenes parciales, el proyecto y la participación —, al total. ¡Para los estudiantes, es fácil entender que es buena idea estudiar para el examen final!
Como las gráficas circulares relacionan partes individuales con un todo, normalmente su usan para presupuestos u otros propósitos financieros. Veamos el ejemplo del presupuesto de una familia. Se ha graficado de dos maneras: primero usando una gráfica de barras, y luego usando una gráfica circular. Cada representación ilustra la información de manera distinta.
La gráfica de barras muestra las cantidades de dinero gastadas en cada rubro durante un mes. Usando estos datos, puedes averiguar cuánto necesita ganar la familia al mes para quedar dentro del presupuesto.

La gráfica de barras anterior se centra en la cantidad gastada por cada categoría. La gráfica circular abajo muestra cómo se relaciona cada pieza del presupuesto con las otras piezas. Esto hace más fácil ver a dónde se van las cantidades grandes de dinero, y cuánto del presupuesto total toman dichas piezas. La renta y la comida son los gastos más grandes, y el cuidado de los niños también toman una porción considerable.
Si observas detenidamente la gráfica circular, puedes ver que las secciones para la comida, cuidado de los niños y utilidades toman casi la mitad del círculo — ¡esto significa que estos tres rubros representan la mitad del presupuesto! Este tipo de análisis es más difícil de hacer con gráficas de barras porque cada rubro se representa como su propia entidad, y no es parte de un todo.

Las gráficas circulares normalmente muestran la relación de cada pieza con el todo usando porcentajes, como en el siguiente ejemplo.
| Ejemplo | ||
| Problema | La siguiente gráfica circular muestra cómo Joelle administró su día. ¿Pasó más tiempo durmiendo o haciendo algo relacionado con la escuela (escuela, tarea y ensayo de la obra)?
| |
|
| Dormir: 36%
Relacionado con la escuela: 27% + 8% + 11% = 46%
| Observa la gráfica circular. La sección marcada como “Dormir” Es un poco más grande que la sección “Escuela” (¡y observa que el porcentaje de tiempo de dormir es más grande que el porcentaje de tiempo en la escuela!) “Tarea” y “Ensayo de la obra” son más pequeñas, pero cuando se suman los porcentajes de tiempo a “Escuela”, la suma resulta la mayor porción del día. |
| Respuesta | Joelle pasó más tiempo haciendo cosas relacionadas con la escuela. | |
| La gráfica siguiente muestra datos sobre cómo se trasladan diariamente los trabajadores de una compañía.
¿Cuál es el enunciado verdadero?
A) Todos usan el carro, el autobús o el tren para ir a trabajar. B) Tomar el autobús es más popular que caminar o montar en bicicleta. C) Más personas toman el tren que el autobús. D) Trabajar desde casa es el método menos popular.
|
A diferencia de las gráficas circulares, las gráficas lineales normalmente se usan para relacionar datos con un periodo de tiempo. En una gráfica lineal, los datos se muestran como puntos individuales en una cuadrícula: una línea de tendencia conecta todos los puntos.
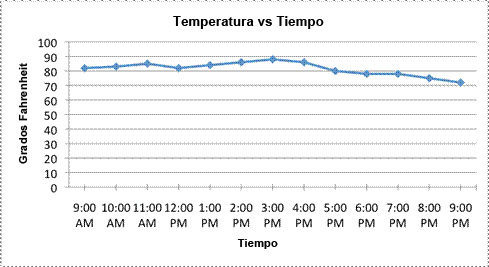
Un uso típico de una gráfica lineal consiste en mapear la temperatura con el tiempo. Un ejemplo se muestra a continuación. Observa cómo la temperatura se mapea en el eje-y el tiempo en el eje-x.
Cada punto en la cuadrícula muestra la relación específica entre la temperatura y el tiempo. A las 9:00 AM, la temperatura fue de 82, se elevó a 83º a las 10:00 AM, y luego de nuevo a 85º a las 11:00 AM. Se enfrió un poco por la tarde, pues la temperatura cayó a 82º. ¿Qué pasó en el resto del día?
Los datos en la gráfica muestran que la temperatura llegó a su máximo de 88º a las 3:00 PM. Como a las 9:00 PM de la tarde, bajó a 72º.
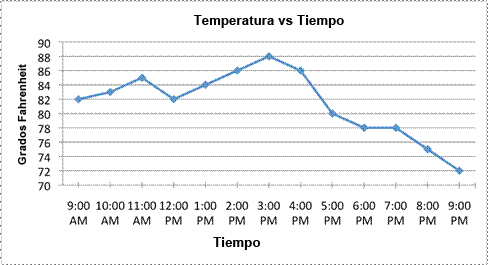
Hay que considerar también los segmentos de línea que conectan cada punto. Si bien la gráfica sólo provee puntos de datos para cada hora, podrías conocer la temperatura cada minuto (¡o segundo!) si quisieras. Los segmentos de línea que conectan los puntos de datos indican que la relación entre la temperatura y el tiempo es continua: se puede leer en cualquier punto. Los segmentos de línea también proveen un estimado de qué temperatura hubiera marcado el termómetro si se hubiera medido en cierto momento entre dos lecturas existentes. Por ejemplo, si quisieras estimar la temperatura a las 4:30, podrías encontrar 4:30 en el eje-x y dibujar una línea vertical que pase a través de la línea de tendencia; el lugar donde se intersecta será la temperatura estimada a esa hora.
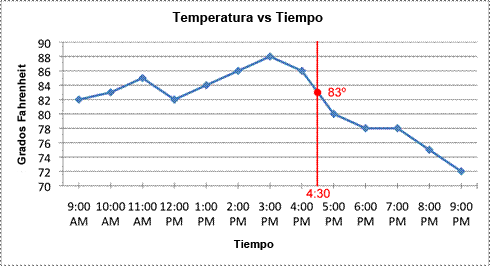
Observa que esto es sólo un estimado basado en los datos: existen muchas posibles fluctuaciones de temperatura entre las 4:00 PM y las 5:00 PM. Por ejemplo, la temperatura se pudo haber mantenido a 86º la mayor parte de la hora, y luego caer de repente a 80º minutos antes de las 5:00 PM. Alternativamente, la temperatura pudo haber caído a 76º debido a una tormenta, y luego subir de nuevo a 80º una vez pasada la tormenta. ¡En cualquiera de los casos, nuestro estimado de 83º será incorrecto! Basados en los datos, 83º parece una predicción razonable para las 4:30 PM.
Finalmente, un comentario rápido sobre la escala de la gráfica. Observa que el eje y ( la línea vertical donde se marcan los Grados Fahrenheit), empieza a los 70º y luego aumenta en incrementos de 2º. Como la escala es pequeña y la gráfica empieza a los 70º, la temperatura se ve un poco volátil, ¡como si la temperatura fuera de caliente a muy frío! Observa los mismos datos cuando se grafican en una gráfica lineal que empieza a los 0º y tiene una escala de 10º. ¡Los picos y valles no son tan aparentes!
Como puedes ver, cambiar la escala de la gráfica puede afectar la forma en la que percibimos los datos.
| Ejemplo | |
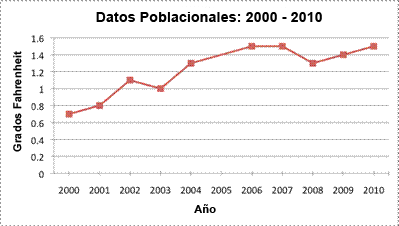
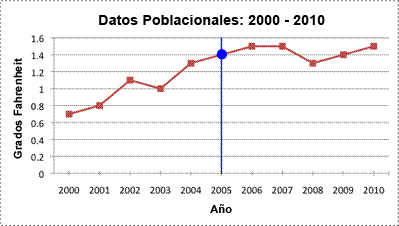
| Problema | Se proporcionan datos ficticios de la población de una ciudad. Estimar la población en el año 2005.
|
|
| Observa la línea en la gráfica. La población empieza alrededor de los 0.7 millones (o 700,000) en 2000, se eleva a 0.8 millones en 2001, y se eleva de nuevo a 1.1 millón en 2002. Para calcular la población en el 2005, encuentra el 2005 en el eje-x y dibuja una línea vertical que intersecte la línea de tendencia.
|
|
| La línea se intersecta a los 1.4, entonces 1.4 millones (o 1,400,000) serían un buen estimado. |
| Respuesta | La población en el 2005 fue de alrededor de 1.4 millones. |
Una gráfica de tallo-hoja provee otra manera de visualizar datos cuantitativos. Retienen los datos originales (a diferencia de los pictogramas), y permiten una fácil identificación de los valores máximo y mínimo, cúmulos y vacíos.
Aquí hay un ejemplo. Un economista se pregunta sobre la cantidad de cambio que trae la gente consigo, y si la cantidad es mayor en la mañana que en la tarde. Para recolectar los datos, se va a una estación del metro en el centro una mañana, y le pregunta a las personas al azar cuánto cambio traen. Los resultados se muestran en la tabla.
Cambio (en ¢)
| 0 | 85 | 95 |
| 50 | 44 | 81 |
| 12 | 25 | 25 |
| 15 | 10 | 5 |
| 0 | 76 | 0 |
| 59 | 75 | 73 |
| 4 | 94 | 62 |
| 42 | 0 | 60 |
| 75 | 15 | 25 |
| 31 | 38 | 50 |
La economista quiere entender mejor los datos, por lo que crea una gráfica de tallo-hoja. En esta gráfica, el “tallo” es el dígito de las decenas de cada pieza de datos y la “hoja” es el dígito de las unidades. (Si tuviera que graficar un número de tres dígitos, el tallo tendría dos dígitos y la hoja tendría un dígito. El objetivo en la gráfica de hoja-tallo es que las hojas no contengan más de 10 dígitos del del 0 al 9.)
Empieza listando los valores del tallo, que son todos los dígitos posibles de las decenas: los números del 0 al 9.
| Tallo | Hoja |
| 0 |
|
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
Luego revisa sus datos. La primera persona dijo que traía 0¢; el tallo es 0, y la hoja también es 0 (es importante incluir el 0 para mostrar que fue recolectado como dato).
| Tallo | Hoja |
| 0 | 0 |
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
Vemos las dos siguientes piezas de datos: 50 y 12. Escribimos los datos en la gráfica.
| Tallo | Hoja |
| 0 | 0 |
| 1 | 2 |
| 2 |
|
| 3 |
|
| 4 |
|
| 5 | 0 |
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
El siguiente dato es 15. El tallo es 1 y la hoja es 5, entonces ponemos el 5 junto al 2 que ya estaba en la sección de la hoja de la gráfica.
| Tallo | Hoja |
| 0 | 0 |
| 1 | 2 5 |
| 2 |
|
| 3 |
|
| 4 |
|
| 5 | 0 |
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
Continuamos añadiendo datos hasta que llenemos la gráfica de tallo-hoja.
| Tallo | Hoja |
| 0 | 0 0 0 0 4 5 |
| 1 | 0 2 5 5 |
| 2 | 5 5 5 |
| 3 | 1 8 |
| 4 | 2 4 |
| 5 | 0 0 9 |
| 6 | 0 2 |
| 7 | 3 5 5 6 |
| 8 | 1 5 |
| 9 | 4 5 |
De la gráfica, podemos ver que la mitad de la gente traía menos de 40¢ (como hay 30 piezas de datos, el número medio es el promedio del 15vo y el 16vo objeto. El 15vo objeto es 38 y el 16vo es 42, por lo que la media es 40.) Los datos están bastante esparcidos; al parecer no hay un patrón discernible sobre cuánto cambio trae la gente.
Esa misma tarde, la economista colecta datos de otras 30 personas. En lugar de hacer una nueva gráfica de tallo-hoja, arreglamos la gráfica original y añadimos los datos nuevos creando un nuevo conjunto de hojas, como se muestra a continuación.
| Hoja (Mañana) | Tallo | Hoja (Tarde) |
| 0 0 0 0 4 5 | 0 | 0 0 0 5 |
| 0 2 5 5 | 1 | 0 5 |
| 5 5 5 | 2 | 2 5 5 8 |
| 1 8 | 3 | 0 2 |
| 2 4 | 4 | 5 5 |
| 0 0 9 | 5 | 5 |
| 0 2 | 6 |
|
| 3 5 5 6 | 7 | 0 0 5 6 |
| 1 5 | 8 | 1 1 3 6 8 |
| 4 5 | 9 | 0 5 8 8 8 9 |
Observamos que la forma de los datos de la tarde es diferente que la forma de los datos de la mañana. En la mañana, mucha gente traía menos de 40¢. Sin embargo, en la tarde, la gente parecía traer más cambio, con la mitad de las personas trayendo entre 70¢ y 99¢.
| Ejemplo | ||||||||||||||
| Problema | Un biólogo usa una gráfica de tallo-hoja para registrar las edades (en años) de diez árboles en un bosque. ¿Cuántos años tenían los árboles que registró?
| |||||||||||||
|
|
| Para leer la gráfica de tallo-hoja, observamos el tallo, y luego la hoja. La primera pieza de datos tiene un tallo de 5 y una hoja de 2. Este es el número 52. | ||||||||||||
|
|
| La segunda pieza de datos tiene un tallo de 5 y una hoja de 4. Este es el número 54. | ||||||||||||
|
|
| Continuamos leyendo los tallos y las hojas de la gráfica. | ||||||||||||
| Respuesta | Las edades de los árboles son 52, 54, 54, 66, 80, 81, 84, 86, 95, y 99. | |||||||||||||
| ¿Qué conjunto de números representa la gráfica de tallo-hoja?
A) 0, 9, 13, 13, 16, 20, 35, 37, 37, 39 B) 0, 0, 3, 3, 5, 6, 7, 7, 9, 9 C) 0, 9, 13, 16, 20, 35, 37, 39 D) 0, 2, 31, 31, 53, 61, 73, 73, 90, 93
|
Sumario
Las gráficas de barras son sólo el inicio de la historia cuando se trata de visualizar conjuntos de datos. Las gráficas circulares muestran cómo un conjunto de datos se divide en secciones, y nos ayudan a visualizar cómo cada sección se relaciona con el todo. En contraste, las gráficas lineales normalmente se usan para relacionar datos continuos sobre un periodo de tiempo. Un tercer tipo de gráfica, la gráfica tallo-hoja, provee otra forma de organizar datos cuantitativos. Las gráficas de tallo-hoja son útiles para tener una idea rápida de los valores más grandes y los más pequeños, cúmulos y huecos en los datos del conjunto.