Figuras en 1 y 2 dimensiones
Objetivos de aprendizaje
· Identificar y definir puntos, rectas, segmentos de recta, rayos y planos.
· Clasificar ángulos en agudos, rectos, obtusos, o rectos.
Introducción
Utilizamos términos geométricos en el lenguaje cotidiano, muchas veces sin darnos cuenta. Por ejemplo, cada vez que dices “caminas en línea recta” o “cuidado, ésta calle hace ángulo recto” estás usando términos geométricos para describir lo que te rodea Utilizas estos términos de manera flexible, y las personas generalmente saben de lo que estás hablando.
En el mundo de las matemáticas, cada uno de estos términos geométricos tiene una definición específica. Es importante conocer dichas definiciones — así como la construcción de distintas figuras — para familiarizarte con el lenguaje de la geometría. Empecemos con la figura geométrica básica: el plano.
Un plano es una superficie plana que continúa por siempre (o, en términos matemáticos, indefinidamente) en todas direcciones. Tiene dos dimensiones: largo y ancho.
Puedes visualizar un plano al poner una hoja de papel sobre una mesa. Ahora imagina que la hoja permanece perfectamente plana y se extiende hasta donde alcanza la vista en todas direcciones, de izquierda a derecha y de arriba a abajo. Esta gigantesca hoja de papel te da una idea de lo que es un plano geométrico: continúa indefinidamente en dos direcciones. (A diferencia de la hoja de papel que usaste, un plano geométrico no tiene altura.)
Un plano puede contener figuras geométricas. La figura geométrica básica es el punto, que no tiene dimensiones. Un punto es simplemente un lugar en el plano. Tres puntos que no forman una línea recta, determinan un plano.
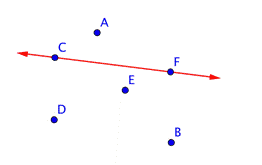
La imagen siguiente muestra cuatro puntos, etiquetados A, B, C, y D.

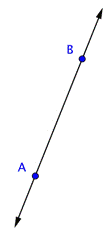
Dos puntos en un plano determinan una recta. Una recta es una figura de una dimensión que está hecha de un número infinito de puntos individuales colocados uno al lado del siguiente. En geometría, todas las rectas se asumen lineales; si doblan, se les conoce como curvas. Una recta continúa indefinidamente en dos direcciones.
Abajo hay una recta AB o, en notación geométrica, ![]() . Las flechas indican que la recta continúa infinitamente en las dos direcciones. La recta también podría llamarse BA. Si bien el orden de los puntos no importa en una recta, se acostumbra nombrar los puntos en orden alfabético.
. Las flechas indican que la recta continúa infinitamente en las dos direcciones. La recta también podría llamarse BA. Si bien el orden de los puntos no importa en una recta, se acostumbra nombrar los puntos en orden alfabético.
La figura siguiente muestra los puntos A y B y la recta ![]() .
.
| Ejemplo | ||
| Problema | Nombra la recta mostrada en rojo. |
|
|
|
| La recta en rojo va desde los puntos C y F, por lo que se llama
|
| Respuesta |
|
|
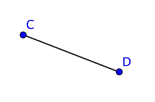
Existen otras dos figuras a considerar. La sección entre dos puntos en una recta se llama segmento de recta. Un segmento de recta puede ser muy largo o muy corto. La diferencia entre una recta y un segmento de recta es que el segmento de recta tiene dos puntos en donde termina y la recta continúa infinitamente. Un segmento de recta se denota por sus dos puntos extremos, como en ![]() .
.
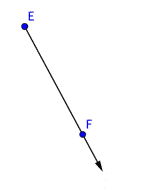
Un rayo tiene un punto extremo pero continúa por siempre en la otra dirección. Los matemáticos llaman a un rayo con la notación ![]() , donde el punto E es el punto extremo y F es un punto en el rayo. Cuando nombramos un rayo, siempre decimos primero el punto extremo. Observa que
, donde el punto E es el punto extremo y F es un punto en el rayo. Cuando nombramos un rayo, siempre decimos primero el punto extremo. Observa que ![]() tendrá el punto extremo en F, y continúa hasta E, lo que es un rayo distinto a
tendrá el punto extremo en F, y continúa hasta E, lo que es un rayo distinto a ![]() , que tendría el punto extremo en E, y continúa hasta F.
, que tendría el punto extremo en E, y continúa hasta F.
El término “rayo” puede sonar familiar porque es una palabra común en Español. La palabra “rayo” se usa normalmente cuando hablamos de luz. Si bien un rayo de luz se parece al término geométrico “rayo,” no continúa por siempre, y sí tiene un ancho. Un rayo geométrico, no tiene ancho; solo largo.
A continuación se muestra una imagen del rayo EF o ![]() . Observa que el punto extremo es E.
. Observa que el punto extremo es E.
| Ejemplo | ||
| Problema | Identifica cada recta y segmento de recta en la figura. | |
|
|
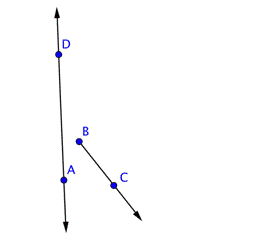
| Dos puntos definen una recta, y una recta se denota con flechas. Hay dos rectas en la figura:
Un segmento de recta es una sección entre dos puntos. |
| Respuesta | Rectas: Segmentos de recta: |
|
| Ejemplo | ||
| Problema | Identifica cada punto y rayo en la figura. | |
|
|
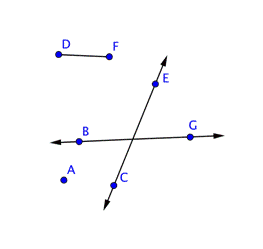
| Hay cuatro puntos: A, B, C, y D.
Hay también tres rayos, aunque sólo uno es obvio.
El rayo
|
| Respuesta | Puntos: A, B, C, D Rayos: |
|
| ¿Cuál de los siguientes no está representado en la imagen?
A) B) C) D)
|
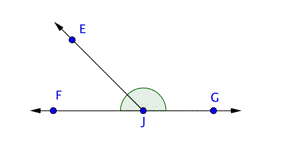
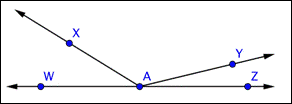
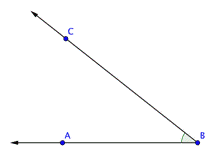
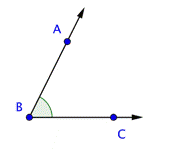
Las rectas, segmentos de recta, puntos, y rayos como bloques de construcción para otras figuras. Por ejemplo, dos rayos con un punto extremo común forman un ángulo. El punto extremo del ángulo se llama vértice.
El ángulo ABC se muestra a continuación. Este ángulo también puede llamarse ![]() ,
, ![]() o simplemente
o simplemente ![]() . Cuando nombres ángulos, ten cuidado de incluir el vértice (aquí, el punto B) como la letra central.
. Cuando nombres ángulos, ten cuidado de incluir el vértice (aquí, el punto B) como la letra central.
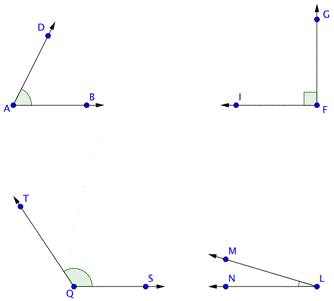
La imagen siguiente muestra algunos ángulos en un plano. Observa que la etiqueta de cada ángulos se escribe como “punto-vértice-punto,” y la notación geométrica está en la forma de ![]() .
.
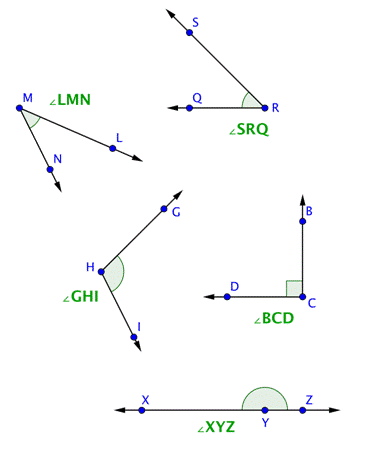
Algunas veces, los ángulos son muy estrechos y otras son muy amplios. Cuando las personas hablan del “tamaño” de un ángulo, se refieren al arco entre los dos rayos. La longitud de los rayos no tiene nada que ver con el tamaño del ángulo. Cuando dibujamos ángulos normalmente incluimos un arco (como se muestra en la figura anterior) para ayudar al lector a identificar el ‘lado’ correcto del ángulo.
Piensa en la carátula de un reloj de manecillas. Las agujas de las horas y los minutos están fijas a un punto en el centro del reloj. Conforme pasa el tiempo, las manecillas rotan alrededor del punto fijo, creando ángulos grandes y pequeños. La longitud de las manecillas no tiene nada que ver con el ángulo que crean.
Un ángulo se mide en grados, representados por el símbolo º. Un círculo tiene 360º. (En patineta y basquetbol, “hacer un 360” significa saltar y hacer una rotación completa del cuerpo.
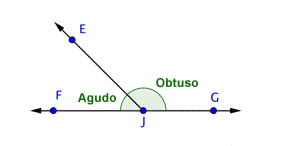
Un ángulo recto es un ángulo que mide exactamente 90º. Representa exactamente un cuarto de vuelta a un círculo. Los rectángulos contienen exactamente cuatro ángulos rectos. Una marca con forma de esquina denota que un ángulo es recto, como se muestra abajo en el ángulo recto DCB.
Los ángulos que miden entre 0º y 90º (más pequeños que los ángulos rectos) se llaman ángulos agudos. Los ángulos que van de 90º a 180º (más grandes que los ángulos rectos pero menores a 180º) se llaman ángulos obtusos. Y un ángulo que mide exactamente 180º se llama ángulos llanos ¡porque nos recuerdan a una superficie plana!
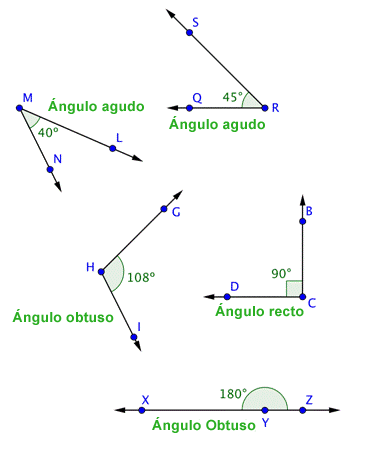
| Ejemplo | ||
| Problema | Etiqueta cada ángulo como agudo, recto, u obtuso en la siguiente figura. | |
|
|
| Puedes empezar identificando los ángulos rectos.
Los ángulos agudos serán menores que
|
| Respuesta |
|
|
| Ejemplo | ||
| Problema | Identifica cada punto, rayo, y ángulo en la siguiente figura. | |
|
|
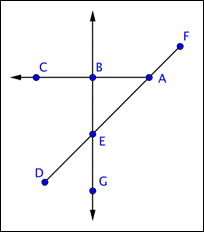
| Empieza identificando cada punto en la figura. Hay 4: E, F, G, y J. |
|
|
| Ahora encuentra los rayos, Un rayo empieza en un punto, y continúa hasta otro punto hacia el infinito (indicado por una flecha. Hay tres rayos que salen del punto J: |
|
|
| Finalmente, busca ángulos. |
| Respuesta | Puntos: E, F, G, J Rayos: Ángulos: |
|
| Identifica los ángulos agudos en la imagen siguiente.
A) B) C) D)
|
Midiendo ángulos con un transportador
Aprender a medir ángulos te puede ayudar a sentirte más cómodo identificando la diferencia entre las medidas de los ángulos. Por ejemplo, ¿cómo se diferencia un ángulo de 135º con un ángulo de 45º?
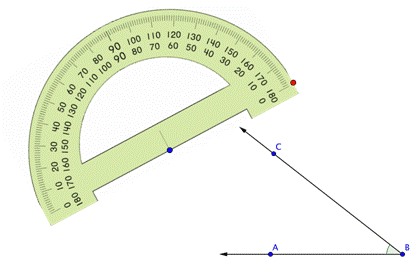
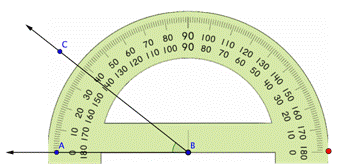
Para medir un ángulo necesitamos un transportador, que es una herramienta semicircular que contiene 180 marcas. Cada marca representa 1º. (Imagínalo así: un círculo tiene 360º, entonces un semicírculo tiene 180º) Para usar el transportador, observa los siguientes pasos:
1. alinea el vértice del ángulo con el punto en el centro del lado recto del transportador,
2. alinea un lado del ángulo con la recta del transportador que tiene la marca de cero, y
3. observa la sección curva del transportador para leer la medida.
Para practicar el uso del transportador, intenta la actividad siguiente:
El ejemplo siguiente muestra cómo usar el transportador para medir el tamaño de un ángulo.
| Ejemplo | |
| Problema | Usa un transportador para medir el ángulo siguiente.
|
|
|
Usa un transportador para medir el ángulo. |
|
|
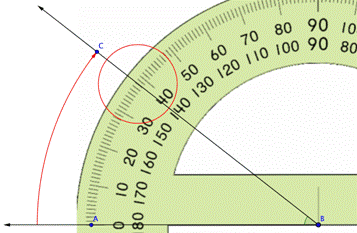
Alinea el punto azul en el transportador con el vértice del ángulo que quieres medir. |
|
|
Rota el transportador alrededor del vértice del ángulo hasta que el lado del ángulo se alinee con el grado 0 de la marca del transportador. |
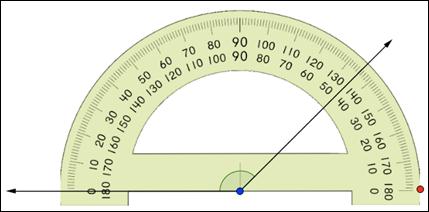
|
|
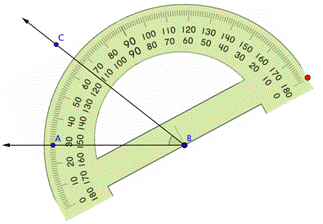
Lee la medida, en grados, del ángulo. Empieza por el lado del ángulo que está alineado con la marca 0º del transportador y cuenta desde 0º, Este ángulo mide 38º. |
| Respuesta | El ángulo mide 38º. |
| ¿Cuál es la medida del ángulo mostrado a continuación?
A) 45º B) 135º C) 145º D) 180º
|
Sumario
Las formas y las figuras geométricas nos rodean. Un punto es un objeto sin dimensiones que define un lugar específico en un plano. Una recta está hecha de un número infinito de puntos, todos alineados uno junto al otro en un patrón recto y que continúa por siempre. Un rayo inicia en un punto y va hacia el infinito en una dirección solamente. Un plano puede describirse como una superficie infinita de dos dimensiones.
Cuando dos rayos comparten un punto extremo, se forma un ángulo. Los ángulos pueden describirse como agudos, rectos, obtusos y llanos, y se miden en grados. Puedes usar un transportador (una herramienta matemática) para medir el tamaño de un ángulo.