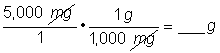Convirtiendo en el sistema métrico
Objetivo de aprendizaje
· Realizar cálculos aritméticos en las unidades métricas de longitud, masa y volumen.
Introducción
Si bien es importante conocer las distintas unidades del sistema métrico, el propósito real de estudiarlo es que podamos utilizar sus unidades métricas para calcular el tamaño, la masa, o el volumen de distintos objetos. En la práctica, normalmente es necesario convertir de una unidad métrica a la otra — esto sucede frecuentemente en los campos de la medicina, la ciencia, y la tecnología, donde el uso del sistema métrico es común.
Si tienes una receta de 5,000 mg de medicina, y al momento de despacharla, la dosis dice 5 g de medicina, ¿cometió un error el farmaceuta?
Por un momento, imagina que eres el farmaceuta Recibes tres prescripciones de amoxicilina líquida: una dice 2.5 centilitros, otra dice 0.3 decilitros, y la otra dice 450 mililitros. La medicina se guarda en el refrigerador en contenedores de 1 litro, 1 decilitro, y un centilitro. ¿Qué contenedor deberías usar para asegurarte que no estás desperdiciando medicina que no se usó?
Para resolver éste problema, necesitas saber cómo convertir de una medida a otra, así como la forma de sumar cantidades diferentes. Veamos cómo se hace esto.
Convertir entre medidas del sistema métrico es simplemente cuestión de identificar la unidad que tienes, la unidad a la que quieres convertir, y luego contar el número de unidades entre ellas. Un ejemplo básico se muestra a continuación.
| Ejemplo | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Problema | Convierte 1 kilómetro a decímetros. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
| Identifica el lugar de los kilómetros y de los decímetros. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
| Los kilómetros (km) son más grandes que los decímetros (dm), por lo que esperas que habrá más de un dm en un km. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
| Cuenta las unidades intermedias mientras vas multiplicando por 10.
(Como vas de una unidad grande a una chica, debes multiplicar.) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| 1 km · 10 · 10 · 10 · 10 = 10,000 dm | Multiplica para encontrar el número de decímetros en un kilómetro. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Respuesta | 1 kilómetro = 10,000 decímetros |
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
El problema es fácil de resolver porque estamos convirtiendo 1 kilómetro a otra unidad. El ejemplo siguiente muestra cómo debes resolver el problema si se te pide convertir 8.2 kilómetros a decímetros. Observa que la mayoría de los pasos son los mismos; la diferencia consiste en que multiplicas por 8.2 en el último paso.
| Ejemplo | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Problema | Convierte 8.2 kilómetros a decímetros. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
| Identifica el lugar de los kilómetros y de los decímetros. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
| Los kilómetros (km) son más grandes que los decímetros (dm), por lo que esperas que habrá más de un dm en un km. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
| Cuenta las unidades intermedias mientras vas multiplicando por 10.
(Como vas de una unidad grande a una chica, debes multiplicar.) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| 8.2 km · 10 · 10 · 10 · 10 = 82,000 dm | Multiplica para encontrar el número de decímetros en 8.2 kilómetros. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Respuesta | 8.2 kilómetros = 82,000 decímetros |
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
También puedes utilizar las reglas de la base 10 “recorrer el decimal” en el ejemplo. Nota cómo los decímetros (dm) están cuatro lugares a la derecha de los kilómetros (km); de manera similar, mueves el punto decimal cuatro lugares a la derecha cuando conviertes 8.2 kilómetros a decímetros.
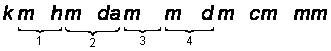
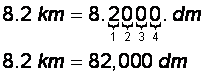
| Ejemplo | ||
| Problema | Convierte 0.55 litros a centilitros. | |
|
|
| Cuenta dos lugares desde litros a centilitros. |
|
|
| En 0.55 l, mueve el punto decimal dos lugares hacia la derecha. |
|
|
|
|
| Respuesta | 0.55 litros = 55 centilitros |
|
| ¿Cuántos decalitros hay en 0.5 decilitros?
A) 500
B) 5
C) 0.5
D) 0.005
|
Convirtiendo de unidades chicas a unidades grandes
Puedes realizar el mismo proceso para convertir de unidades chicas a unidades grandes. Cuando conviertes una unidad grande a una chica, multiplicas; cuando conviertes de una unidad chica a una grande, divides. Veamos un ejemplo.
| Ejemplo | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Problema | Convierte 739 centigramos a gramos. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
| Identifica el lugar de los centigramos y de los gramos. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
| Los centigramos (cg) son más chicos que los gramos (g), por lo que se espera que haya menos que 739 g en 739 cg. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
| Cuenta las unidades intermedias, mientras que vas dividiendo entre 10.
(Como vas de una unidad chica a una grande, debes dividir.) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| 739 ÷ 10 ÷ 10 = 7.39 g | Divide para encontrar el número de gramos en 739 centigramos. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Respuesta | 739 centigramos = 7.39 gramos |
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Observa que el método de contar prefijos y recorrer el punto decimal también funciona aquí. Sólo asegúrate que estás moviendo el punto decimal en la dirección correcta para la conversión.
| Ejemplo | ||
| Problema | Convierte 205.5 mililitros a kilolitros. | |
|
|
| Cuenta seis lugares desde mililitros a kilolitros. |
|
|
| Los mililitros son más chicos que los kilolitros, por lo que se espera que el número 205.5 vaya disminuyendo al moverte en la tabla métrica.
En 205.5 ml, mueve el punto decimal seis lugares hacia la izquierda. |
|
|
|
|
| Respuesta | 205.5 mililitros = 0.0002055 kilolitros | |
| Convierte 3,085 miligramos a gramos.
A) 3,085,000 gramos
B) 308.5 gramos
C) 3.085 gramos
D) 0.3085 gramos
|
El método de cancelación de unidades
Existe otro método que puedes usar para convertir unidades métricas — el método de cancelación de unidades. Utilizaste éste método cuando convertías unidades de medida del sistema métrico tradicional de los Estados Unidos.
El método de cancelación de unidades funciona también en el sistema métrico; se basa en el uso de fracciones de unidad y la cancelación de unidades intermedias. La tabla siguiente muestra algunas de las unidades equivalentes y fracciones de unidad para longitud en el sistema métrico. (Debes notar que todas las fracciones de unidades contienen el factor 10. Recuerda que el sistema métrico se basa en la noción de que cada unidad es 10 veces más grande que la unidad anterior.)
También, observa que hay dos prefijos nuevos: mega- (que es muy grande) y micro- (que es muy chico).
| Unidades equivalentes | Factores de conversión
| |
| 1 metro = 1,000,000 micrómetros |
|
|
| 1 metro = 1,000 milímetros |
|
|
| 1 metro = 100 centímetros |
|
|
| 1 metro = 10 decímetros |
|
|
| 1 decámetro = 10 metros |
|
|
| 1 hectómetro = 100 metros |
|
|
| 1 kilómetro = 1,000 metros |
|
|
| 1 megámetro = 1,000,000 metros |
|
|
Cuando aplicamos el método de cancelación de unidades en el sistema métrico, ¡asegúrate de no estar saltándote unidades intermedias de medida!
| Ejemplo | ||
| Problema | Convierte 7,225 centímetros a metros. | |
|
| 7,225 cm = ___ m | Los metros son más grandes que los centímetros, por lo que esperamos que la respuesta sea menor que 7,225. |
|
|
| Usando el método de cancelación de unidades, escribe 7,225 cm como una fracción y utiliza unidades equivalentes para convertir a m. |
|
|
| Cancelar unidades similares, multiplicar y simplificar. |
| Respuesta | 7,225 centímetros = | |
| Utiliza el método que prefieras para convertir 32.5 kilómetros a metros.
A) 32,500 m
B) 325 m
C) 0.325 m
D) 0.00325 m
|
Ahora que ya hemos visto cómo convertir entre unidades métricas de varias maneras, veamos el problema del principio.
| Ejemplo | ||
| Problema | Si tienes una receta de 5,000 mg de medicina, y al momento de despacharla, la dosis dice 5 g de medicina, ¿cometió un error el farmaceuta? | |
|
| 5,000 mg = ___ g? | Necesitamos convertir mg a g. |
|
|
|
|
| Respuesta | 5 g = 5,000 mg, el farmaceuta no cometió un error. | |
Sumario
Para convertir entre unidades del sistema métrico, identificamos la unidad que tenemos, la unidad a la que queremos convertir, y luego contamos el número de unidades entre ellas. Si convertimos de una unidad grande a una más chica, multiplicamos sucesivamente por 10. Si convertimos de una unidad chica a una más grande, dividimos sucesivamente entre 10. El método de cancelación de unidades también puede aplicarse para las conversiones dentro del sistema métrico. Para usar dicho método, multiplicas la medida original por fracciones de unidad; esto nos permite representar la medida original en una unidad de medida distinta.